A figura abaixo mostra dois ioiôs de mesmo tamanho (raios iguais) e mesma massa, que podem descer rolando por uma corda que os prende ao teto. As cordas são inextensíveis e não deslizam.

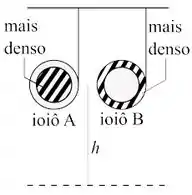
Cada ioiô é composto dos mesmos dois materiais, um mais denso que o outro (ou seja, com uma massa maior por unidade de volume).

No ioiô o material mais denso forma a metade interna da área do disco. No ioiô ele forma a metade externa da área do disco.

Os dois ioiôs são largados a partir do repouso.

Após eles descerem rolando uma mesma altura , o que podemos afirmar sobre as energias cinéticas, e , as velocidades dos centros de massa, e , e as velocidades angulares e dos ioiôs e respectivamente?

Nós temos, nos ioiôs, um problema de rolamento sem deslizamento. A condição para isso é que:

Onde é o raio do ioiô, é a velocidade do centro de massa e é a velocidade angular.

Agora precisamos achar a velocidade do centro de massa. Para isso, nós usamos o princípio da conservação de energia.

No nosso caso, toda a energia potencial gravitacional é transformada em energia cinética de rotação e energia cinética de translação (do centro de massa).

Vamos definir um sistema de coordenadas de forma que corresponde ao instante inicial, e que o sentido do eixo é para cima (oposto ao sentido de movimento dos ioiôs). Isso nos dá:

Enquanto a energia cinética total inicial também é zero, e no final ela é:

Com a condição de não deslizamento, temos:

Juntando tudo na conservação da energia:

Uma primeira observação nesse passo. A variação da energia potencial gravitacional, nos dois casos, é igual, porque ela só depende da massa dos ioiôs e da distância percorrida. Pela conservação da energia:

Então, a variação da energia cinética para ambos é igual. Eles partem do repouso, o que significa que , e por isso a energia cinética de ambos os ioiôs vai ser a mesma.