Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Cinética de Rotação

Ver Teoria
Exercício 441234567891011121314151617181920212223242526272829303132333435363738394041424345464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899

Enunciado

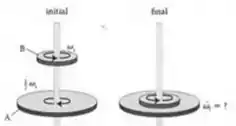
O disco A na figura abaixo, com raio R e inércia m está inicialmente rodando na direção horária, como visto de cima com uma velocidade angular ω i / 2 . O disco B , de inércia m B = 3 m e raio R B = R / 2 , está inicialmente rodando na direção anti-horária com velocidade angular ω i . Os dois discos estão restritos a rodar em torno do mesmo eixo, que passa pelo centro de ambos os discos. Há atrito entre os discos, de forma que após entrarem em contato os discos giram com a mesma velocidade angular ω f .

  1. Qual é a velocidade angular final, ω f , do sistema?
  2. Determine a variação de energia térmica do sistema composto pelos dois discos.

Passo 1

L e t r a   A :

POW! Sabemos da teoria que o momento angular L em um sistema fechado e sem interferências de forças externas se conserva, isto é...

L i = L f

O momento angular pode ser calculado por L = I ω , onde I é o momento de inércia da cada disco.

Passo 2

Inicialmente, como os discos estão separados...

L i = L A i + L B i     →

L i = I A ω A i + I B ω B i     →

Só que cara, o problema nos disse que a velocidade angular do disco A é ω i / 2 . No sentido horário vista de cima para baixo. Enquanto isso, o disco B gira com veloidade angular ω i ...

L i = I A - ω i / 2 + I B ω i     →

O valor do menos é só para indicar que os discos giram em sentidos opostos.

Agora, quem vem a ser I A e I B ?

Passo 3

Como já falamos I representa o momento de inércia. No caso, é o momento de inércia de discos girando ao redor do eixo que passa pelo centro. De acordo com a teoria, para esse cara...

I = M r 2 2

Então...

I A = m R 2 2  

I B = 3 m R 2 2 2 = 3 m R 2 8

Logo...

L i = I A - ω i / 2 + I B ω i     →

L i = - I A ω i 2 + I B ω i     →

L i = - m R 2 2 ω i 2 + 3 m R 2 8 ω i     →

L i = - m R 2 4 ω i + 3 m R 2 8 ω i     →

L i = m R 2 8 ω i

Passo 4

Agora vejamos o momento final...

L f = I A + I B ω f

Então...

L f = m R 2 2 + 3 m R 2 8 ω f   →

L f = 7 m R 2 8 ω f   →

Como vimos no passo 1...

L i = L f   →

m R 2 8 ω i = 7 m R 2 8 ω f     →

Isolando ω f ...

ω f = 8 7 m R 2 m R 2 8 ω i   →

ω f = 1 7 ω i  

Passo 5

L e t r a   B :

Beleza! Cara... No início tínhamos dois discos girando, e então no início tínhamos apenas energia cinética de rotação...

E i = E A i + E B i

No final, temos o conjunto girando, logo teremos a energia se cinética do sistema girando e, além disso, teremos a no final a energia térmica desprendida no processo ( E t t ). De modo que no final a soma dessas energias será...

E f = E A B f + E t t

Então, como a energia tem que se conservar no sistema...

E A B f + E t t = E A i + E B i   →

E t t = E A i + E B i - E A B f

Então essa será a energia desprendida no processo . Vamos calcula-la?

Passo 6

A energia inicialmente no A vai ser...

E A i = I A ω A 2 2 = m R 2 2 ⋅ - ω i 2 2 2     →

E A i = m R 2 2 ⋅ ω i 2 4 2 = m R 2 16 ω i 2

Para o disco B ...

E B i = I B ω B 2 2 = 3 m R 2 8 ⋅ ω i 2 2   →

E B i = 3 m R 2 16 ω i 2

Agora, para a energia final...

E A B f = I A B ω f 2 2

Onde I A B é o momento de inércia do conjunto ( I A + I B )...

E A B f = 7 m R 2 8 1 7 ω i 2 2     →

E A B f = 7 m R 2 8 1 7 ⋅ 7 ω i 2 2     →

E A B f = m R 2 112 ω i 2  

Então, a energia dissipada em forma de calor vai ser...

E t t = E A i + E B i - E A B f   →

E t t = m R 2 16 ω i 2 + 3 m R 2 16 ω i 2 - m R 2 112 ω i 2   →

E t t = m R 2 4 ω i 2 - m R 2 112 ω i 2   →

E t t = 28 m R 2 4 ⋅ 28 ω i 2 - m R 2 112 ω i 2   →

E t t = 27 m R 2 112 ω i 2

Resposta

Letra A:

ω f = 1 7 ω i

Letra B:

E t t = 27 m R 2 112 ω i 2

Exercícios de Livros Relacionados

Uma régua de um metro é mantida verticalmente com uma das extremidades apoiada no solo e depois liberada. Determine a velocidade da outra extremidade pouco antes de tocar o solo, supondo que a extremi
Na figura abaixo, uma barra fina e homogênea (com 4 m de comprimento e uma massa de 3 k g ) gira livremente em torno de um eixo horizontal A que é perpendicular à barra e passa por um ponto situado a
O corpo rígido da figura abaixo é formado por três bolas e três barras de ligação, com M = 1,6 k g , L = 0,6 m e θ = 30 ° . As bolas podem ser tratadas como partículas e as barras têm massa desprezíve
Como estagiário de uma empresa de engenharia, você é solicitado a medir o momento de inércia de uma grande roda, para girar em torno de um eixo que passa pelo seu centro. Você mede o diâmetro da roda,
91 . Na F I G U R AP D 12.91 , uma bola de gude desce rolando um trilho que possui uma parte em loop com raio R . A bolinha possui massa m e raio r . Que altura mínima h deve ter o trilho a fim de que