A hélice ligada ao rotor de um helicóptero é composta de três lâminas com cada uma tendo comprimento de e massa . O rotor gira a revoluções por minuto. Considere cada lâmina como uma haste fina.

Haste:
a) Calcule o momento de inércia do conjunto das lâminas em torno do eixo de rotação.
b) Determine a energia cinética de rotação desse conjunto de três lâminas.
Passo 1
Para calcular o momento de inércia do conjunto, vamos somar os momentos de inércia de cada lámina.
Como as três lâminas são iguais e estão a uma mesma distância do eixo de rotação, seus momentos de inércia são iguais:
Passo 2
Como calculamos o momento de inércia de cada lâmina ?
Sabemos o momento de inércia de uma haste fina com relação à um eixo perpendicular passando pelo seu centro de massa:
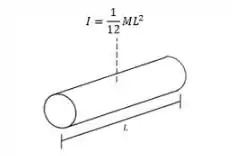
Como o eixo está passando pela extremidade, vamos usar o teorema dos eixos paralelos:
A distância entre os eixos será metado do comprimento da haste:
Passo 3
Voltando ao momento de inércia do conjunto, temos:
Substituindo os valores:
Passo 4
Na letra (b), queremos a energia cinética de rotação .
A energia cinética de rotação será:
Passo 5
Mas como achamos a velocidade angular ?
Sabemos que o conjunto completa revoluções por minuto.
Podemos calcular a velocidade angular com:
O quanto o conjunto girou sobre o intervalo de tempo .
Temos que escrever em radianos. Como uma volta completa respresenta , o deslocamento angular será:
Enquanto o intervalo de tempo será de um minuto:
Assim, temos que:
Passo 6
A energia cinética de rotação será:
Resposta
(a)
(b)