Uma bengala delgada de comprimento é constituída de uma haste homogênea de massa e uma pequena esfera de massa de raio desprezível na extremidade. Inicialmente equilibrada na vertical, ela começa a tombar mantendo o ponto de contato com o solo fixo devido ao atrito estático. Considerando a rotação em torno do eixo perpendicular à figura que passa pelo ponto de contato entre a bengala e o solo, determine a velocidade angular da esfera imediatamente antes de colidir com o solo.
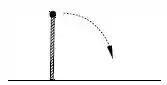
a)
b)
c)
d)
e)
Passo 1
Conservando a energia mecânica do sistema temos que
Substituindo os valores do problema ficamos com
Onde vamos ter que substituir aquele usando o teorema dos eixos parelelos, já que só conhecemos o eixo que passa pelo centro da barra.
Resposta
Exercícios de Livros Relacionados
Uma régua de um metro é mantida verticalmente com uma das extremidades apoiada no solo e depois liberada. Determine a velocidade da outra extremidade pouco antes de tocar o solo, supondo que a extremi
Na figura abaixo, uma barra fina e homogênea (com 4 m de comprimento e uma massa de 3 k g ) gira livremente em torno de um eixo horizontal A que é perpendicular à barra e passa por um ponto situado a
O corpo rígido da figura abaixo é formado por três bolas e três barras de ligação, com M = 1,6 k g , L = 0,6 m e θ = 30 ° . As bolas podem ser tratadas como partículas e as barras têm massa desprezíve
Como estagiário de uma empresa de engenharia, você é solicitado a medir o momento de inércia de uma grande roda, para girar em torno de um eixo que passa pelo seu centro. Você mede o diâmetro da roda,
91 . Na F I G U R AP D 12.91 , uma bola de gude desce rolando um trilho que possui uma parte em loop com raio R . A bolinha possui massa m e raio r . Que altura mínima h deve ter o trilho a fim de que