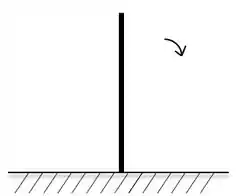
Uma haste uniforme de massa e comprimento é colocada verticalmente acima de um pivô sem atrito, como mostrado na figura abaixo. A partir da vertical, a haste cai para o solo. Com que velocidade a extremidade livre da haste atinge o solo?
A.
B.
C.
D.
E.
Passo 1
A gente quer descobrir qual a velocidade da haste quando ela atingir o solo.
Como não temos forças dissipativas realizando trabalho e roubando energia do nosso sistema, temos que a nossa energia mecânica se conserva!! Uhuuul!
Considerando o centro de massa da barra:
Vamos utilizar a energia cinética rotacional? Sim, pois o movimento da barra vai ser uma rotação;
Mas e aí? Qual é a altura do centro de massa? O CM tá no meio da barra, então .
Então:
Maravilha!
Passo 2
Bom, o momento de inércia de uma barra delgada presa na sua extremidade é dado por:
Além disso, sabemos que a relação entre a velocidade linear do ponto mais extremo da barra e sua velocidade angular é dada por:
Assim, substituindo tudo isso na equação do passo 1:
Simplificando um pouquinho:
Resposta
Alternativa E