Uma placa não-uniforme de massa está inicialmente em repouso no plano vertical, podendo girar sem atrito sobre um eixo perpendicular ao plano que passa pelo ponto .
Seu centro de massa (CM) está a uma altura do eixo, e o ponto em sua extremidade está a uma altura do eixo. Seu momento de inércia em relação ao eixo que passa pelo ponto é .
Partindo do repouso, a placa cai sob efeito da aceleração gravitacional , girando sobre o ponto , conforme a figura.
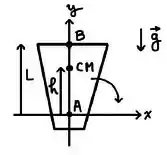
Quando o ponto passa pelo eixo , sua velocidade é:
Passo 1
Um problema desse tipo, de barras em pé que começam a cair devido à gravidade, é aquela coisa né: Conservação da energia, levando em conta a energia cinética de rotação.
Neste caso, a conservação da energia fica:
Como a placa está inicialmente em repouso, sua energia cinética é zero .
Além disso, sua energia potencial tem que ser calculada com base em seu centro de massa!
Pelo enunciado, a altura do centro de massa é . Logo:
No ponto “final” da rotação (que nos interessa) o centro de massa está no eixo , e logo não tem energia potencial gravitacional . Além disso, o corpo estava girando com relação a um eixo perpendicular ao plano que passa pelo ponto A. A energia cinética vai ser:
Onde é a velocidade angular do corpo e é o momento de inércia com relação ao eixo que passa por . Juntando tudo na conservação da energia:
Passo 2
Nós queremos a velocidade linear do ponto quando ele cruza o eixo . Nesse caso, como a distância de até é igual a , podemos relacionar e por:
Substituindo na nossa igualdade do passo anterior:
Tirando a raiz dos dois lados, temos que a resposta é a letra (b).
Resposta
Letra (b)