[ENUNCIADO COMUM ÀS QUESTÕES 5 E 6]
Uma barra delgada de massa e comprimento é mantida na vertical com uma das extremidades apoiada no solo e depois é liberada. A extremidade superior atinge o solo sem que a extremidade de apoio deslize. Considere e que o momento de inércia de uma barra de massa e comprimento em torno de um eixo que passa pelo seu centro de massa é .
[QUESTÃO 6]
Qual é a energia cinética da barra quando ela faz um ângulo com a horizontal?
(a) J
(b) J
(c) J
(d) J
(e) J
(f) J
(g) J
(h) J
(i) J
Passo 1
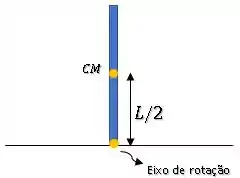
A barra está em rotação em torno de um eixo passando pela sua base, pois ela tomba sem que esse ponto deslize:

Em primeiro lugar, precisamos descobrir o momento de inércia da barra com relação ao seu eixo de rotação.
Então, vamos aplicar o teorema dos eixos paralelos:
Passo 2
A energia cinética da barra será apenas a energia cinética de rotação, pois a barra realiza apenas um movimento de rotação em torno de sua base.
Então, poderíamos calcular essa energia com:
Porém, não sabemos qual é a velocidade angular na situação do problema.
Então, vamos aplicar a conservação de energia mecânica para encontrar a energia cinética da barra.
OBS: Calculamos a energia potencial gravitacional de um corpo extenso a partir da altura de seu centro de gravidade CG, que normalmente coincide com seu centro de massa CM.
Passo 3
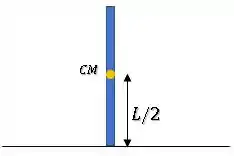
A barra parte do repouso, então, inicialmente, temos apenas uma energia potencial gravitacional relacionada ao seu centro de massa:
Passo 4
Na situação onde a barra faz um ângulo com a horizontal, teremos ainda uma energia potencial gravitacional mas também uma energia cinética associada à sua rotação:

Mas quem será essa altura ?
Podemos relacionar a altura com esse ângulo ...
Olha só:
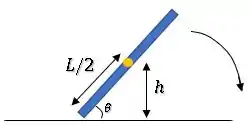
Substituindo na expressão de energia, temos:
Passo 5
Conservando a energia, temos:
Aplicando os valores numéricos, temos:
J
Ficamos com a letra (h).
Resposta
Letra (h)