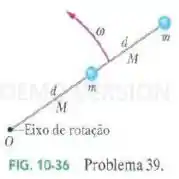
Na Fig. 10-36, duas partículas ambas de massa , estão ligadas uma à outra e a um eixo de rotação em por duas barras finas, ambas de comprimento e massa . O conjunto gira em torno do eixo de rotação com velocidade angular . Em relação a , quais são (a) o momento de inércia do conjunto e (b) a energia cinética do conjunto?
Passo 1
A primeira impressão que temos ao ver esse exercício é que é algo novo, que ainda não vimos, mas vamos olhar agora com mais calma.
Você aprendeu a calcular momento de inércia de um sistema de partículas, certo? Ah, se não aprendeu, não tem problema! Por que eu vou explicar rapidinho aqui!
Ok, temos duas partículas nesse exercício, e você vai fazer o mesmo: somar. Lembrando que o momento de inércia da partícula é dado por:
A parada é que agora temos duas barras, corpos extensos, pertencendo ao mesmo sistema da partícula. O que fazer?

É so somar também! E o momento de inércia da barra é dado por:
Só que no caso da nossa barra que é presa pela extremidade teremos que usar o teorema dos eixos paralelos.
Onde é a massa da barra e é a distância do centro de massa do corpo até o eixo de rotação.
Detalhe que só podemos somar esses momentos de inércia pois as partículas e os corpos rígidos formam um sistema que anda junto e rotaciona ao redor de um mesmo eixo, por isso,
para encontrar o momento de inércia do sistema só precisamos somar o momento de inércia de cada corpo em relação ao eixo de rotação.
Passo 2
a) Temos que fazer o momento de inércia do sistema que é a soma dos momentos de inércia:
Vamos identificar as partes do sistema e as suas distâncias ao eixo:
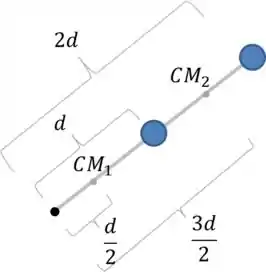
Portanto:
Para barra 1, temos uma barra presa por uma extremidade, então temos que usar o teorema dos eixos paralelos:
Já para a barra 2, precisamos fazer uso do teorema dos eixos paralelos de novo e aqui a distância do eixo é :
Já que temos todos os momentos de inércia vamos para o cálculo do momento de inércia do sistema.
Passo 3
Como o momento de inércia do sistema é a soma dos momentos de inércia de cada componente temos:
Passo 4
Agora com o momento de inércia do sistema, fica moleza para calcular a energia cinética de rotação: