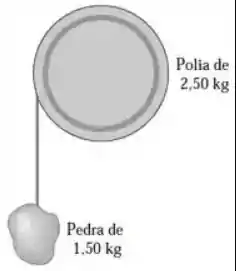
Uma polia sem atrito possui o formato de um disco maciço e uniforme com massa de 2,50 kg e raio de 0,2 m. Uma pedra de 1,5 Kg é presa a um cabo muito leve que envolve a borda da polia, e o sistema é liberado a partir do repouso, imagem abaixo. Qual distância a pedra deve descer para que a polia tenha 4,5 J de energia cinética? Considere o momento de inércia da polia .
Passo 1
Falai galerinha, tudo na paz?
Vamos resolver essa questão utilizando a conservação da energia mecânica.
A energia mecânica total de um sistema é conservada se não houver dissipação de energia. Neste caso, a energia mecânica total do sistema é a soma da energia potencial gravitacional da pedra e a energia cinética da polia.
No início, quando a pedra é liberada do repouso, toda a energia está na forma de energia potencial gravitacional:
Onde:
- é a massa da pedra
- é a aceleração devido à gravidade
- é a altura inicial.
Passo 2
Quando a pedra cai e a polia gira, parte da energia potencial gravitacional da pedra é convertida em energia cinética da pedra, enquanto o restante é convertido em energia cinética da polia e potencial gravitacional da polia.
Quando a polia tem de energia cinética, podemos considerar a altura final da pedra como sendo onde é o raio da polia
A energia cinética da pedra é
A energia cinética da polia é
Para que a polia tenha de energia cinética, a energia final do sistema é a soma das energias cinéticas da pedra e da polia:
Passo 3
A energia final é a soma da energia cinética da pedra e a energia cinética da polia:
Onde:
- é a massa da pedra
- é a velocidade da pedra.
- é o momento de inércia da polia
- é a velocidade angular da polia.
- é a massa da polia
-
Sabemos que a velocidade tangencial da pedra é a mesma que a velocidade tangencial da borda da polia, que é
Portanto:
Substituindo as expressões para
Onde é a velocidade linear da borda da polia.
Passo 4
Agora, igualando a energia inicial à energia final:
Vamos isolar nesta equação:
Onde
Agora, podemos substituir esse valor de na equação de conservação de energia mecânica para encontrar
Passo 5
Substituindo os valores conhecidos:
Vamos calcular a partir desta equação:
Portanto, a altura que a pedra deve cair para que a polia tenha de energia cinética é aproximadamente .