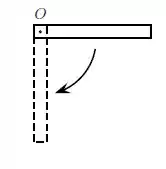
Uma haste fina uniforme e homogênea, de espessura desprezível e comprimento , pode girar livremente em torno de um eixo horizontal que passa pela extremidade da haste e que é perpendicular a ela. Se a haste for liberada na posição horizontal, a partir do repouso, sua velocidade angular quando passar pela posição vertical será igual a
a)
b)
c)
d)
e)
Passo 1
Se fosse um pêndulo, usaríamos o princípio da conservação da energia, mas e agora com uma haste? Usaremos ele também! Só não podemos esquecer que devemos usar a energia cinética de rotação, beleza?
Vamos considerar o zero da energia potencial a do eixo, portanto:
Passo 2
Sabemos que:
Passo 3
Substituindo tudo:
Isolando o :
Resposta
(c)
Exercícios de Livros Relacionados
Uma régua de um metro é mantida verticalmente com uma das extremidades apoiada no solo e depois liberada. Determine a velocidade da outra extremidade pouco antes de tocar o solo, supondo que a extremi
Na figura abaixo, uma barra fina e homogênea (com 4 m de comprimento e uma massa de 3 k g ) gira livremente em torno de um eixo horizontal A que é perpendicular à barra e passa por um ponto situado a
O corpo rígido da figura abaixo é formado por três bolas e três barras de ligação, com M = 1,6 k g , L = 0,6 m e θ = 30 ° . As bolas podem ser tratadas como partículas e as barras têm massa desprezíve
Como estagiário de uma empresa de engenharia, você é solicitado a medir o momento de inércia de uma grande roda, para girar em torno de um eixo que passa pelo seu centro. Você mede o diâmetro da roda,
91 . Na F I G U R AP D 12.91 , uma bola de gude desce rolando um trilho que possui uma parte em loop com raio R . A bolinha possui massa m e raio r . Que altura mínima h deve ter o trilho a fim de que