Seja um corpo na forma de um quadrado de lado composto por hastes finas com massas indicadas na figura. Na figura está também indicado o sistema de coordenadas a ser utilizado. O corpo pode girar livremente sem atrito em torno do eixo e encontra-se em repouso na posição indicada.
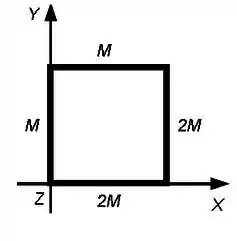
(b) Determine a posição do centro de massa do corpo em função dos dados do problema na posição indicada na figura.
(c) O corpo passa a girar em torno do eixo . Determine o módulo de sua velocidade angular máxima . Em que posição ela ocorre? Suponha que , e .
(d) Determine a velocidade linerar na extremidade do corpo oposta ao eixo na mesma posição do item anterior.
Passo 1
(a)Reduzir à um problema de sistema de partículas
Vamos lembrar da definição de centro de massa? Dá uma olhada:
Fica meio difícil calcular o centro de massa assim, não é mesmo? Quais pontos usaríamos? O truque dessa questão é exatamente entender quais pontos usar. Afinal, não temos como trabalhar com os infinitos pontos dentro de cada haste né.
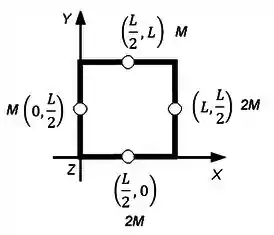
Se as hastes são homogêneas, cada uma isoladamente tem seu próprio centro de massa, que vai ser no exato centro dela! Agora ficou mais simples! Podemos calcular o centro de massa considerando os seguintes 4 pontos:
Passo 2
Calcular
Partindo pras contas, para o , vamos ter:
Passo 3
Calcular
Já para o , vamos ter:
Passo 4
Escrever
Agora é só juntar o que encontramos. Se o centro de massa é , então:
Passo 5
(b)Encontrar o ponto de analisando o movimento do sistema
É sempre uma boa ideia analisar o movimento do sistema antes de tudo. como o quadrado cai, rodando em torno do eixo , vai haver perda de energia potencial gravitacional. Mas claro, essa energia não vai simplesmente desaparecer. Ela vai ser somente convertida! E convertida em energia cinética!
Portanto, a gente pode dizer com segurança e sem medo que ocorre quando é o menor possível, algo que vai acontecer quando a posição do centro de massa for também a menor possível.
Passo 6
Conservação da energia mecânica do centro de massa
Você leu algo sobre forças não conservativas na quest��o? Bem, nem eu. Já que é assim, podemos trabalhar com energia mecânica e a sua conservação:
Sempre que formos trabalhar com a conservação de algo, temos que tomar bastante cuidado com quem chamamos de “”, inicial e “”, final, ok? Isso porque sempre temos que escolher dois pontos com informações conhecidas!
Conhecemos informações do quadrado no repouso e queremos saber informações dele quando é mínimo. Logo:
Passo 7
Substituir valores:
Agora ta fácil. Já temos a expressão da velocidade angular máxima e os valores. Só substituir então!
Passo 8
(d) Calcular a velocidade linear
Lembra dessa expressão simpática?
Com essa pequena fórmula, conseguimos relacionar a velocidade linear com a velocidade angular e a distância do centro de rotação. Para a extremidade do corpo oposta ao eixo , como o corpo é um quadrado, vamos ter que , tudo bem? Aí agora é só calcular:
Onde o termo “” indica que essa velocidade linear pode tanto estar “furando” 
desse plano. Não temos como saber porque não sabemos pra que lado o quadrado girou, beleza? Então vamos deixar indicado.
Resposta
b)
c)
d)