Considere duas esferas sólidas idênticas de massa e raio que são abandonadas do repouso e descem 2 planos inclinados de mesmo comprimento, com a mesma inclinação em relação a direção horizontal. Em um dos planos não há atrito entre a esfera e a superfície. No outro plano há atrito e a esfera desce o plano rolando sem deslizar. É correto afirmar que:
(a) A velocidade do centro de massa da esfera ao atingir a base do plano inclinado será maior no caso em que não há atrito.
(b) A velocidade do centro de massa da esfera ao atingir a base do plano inclinado será a mesma nos dois casos pois a energia mecânica se conserva.
(c) A energia cinética da esfera será maior no caso em que há atrito pois ela possui, nesse caso, velocidade angular de rotação.
(d) Nos caso sem atrito a esfera também rola sem deslizar até a base do plano.
Passo 1
Olhando as alternativas, queremos comparar tanto a energia cinética quanto as velocidades do centro de massa nos dois casos.
Então, o caminho é analisar a energia que conseguiremos essas informações.
Passo 2
Vamos pensar na energia de cada caso.
Inicialmente, temos:
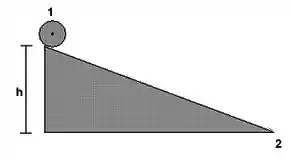
Associada a uma altura as duas esferaras terão uma energia potencial gravitacional .
No plano onde não há atrito, a esfera desliza ao longo do plano, ganhando uma certa velocidade de translação.
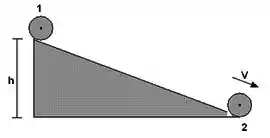
Além disso, a energia mecânica nesse sistema irá se conservar, portanto, toda a energia potencial gravitacional foi convertida em energia cinética de translação :
Passo 3
Já no plano onde há atrito, a esfera não desliza sobre a rampa, ela desce o plano inclinado a partir de um rolamento sem deslizamento, ganhando tanto uma velocidade de translação quanto uma velocidade de rotação.
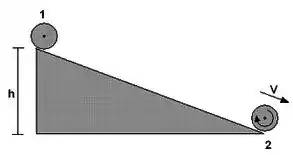
E a energia mecância, se conserva?
Apesar de existir uma força de atrito, não há deslizamente do ponto de contato, então o trabalho da força de atrito é nulo e ela não retira energia do sistema.
Conclusão... a energia mecânica também se conserva nesse sistema.
Porém, diferente do primeiro caso, agora, a esfera ganha uma energia cinética de rotação junto com uma energia cinética de translação:
Passo 4
Como a energia potencial gravitacional foi dividida entre as duas energias cinéticas, a energia cinética de translação no segundo caso é menor que a energia cinética de translação no primeiro caso :
Então, a velocidade de translação (velocidade do centro de massa) da esfera no primeiro caso (sem atrito) será maior que no segundo caso.
Ficamos com a alternativa (a).
Resposta
Letra (a)