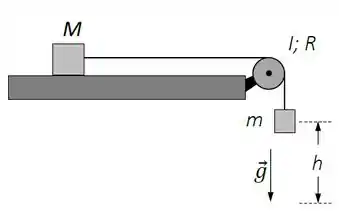
Um bloco de massa encontra-se sobre uma superfície horizontal sem atrito, preso a uma corda que passa por uma roldana circular de raio e momento de inércia (ver Figura 3). A corda não desliza na roldana e sua outra extremidade é presa a um bloco de massa . O sistema encontra-se inicialmente em repouso. Considere .

1. Num dado instante após o sistema ser liberado, os blocos possuem velocidade de módulo . Qual é a velocidade angular da roldana nesse instante? Qual é a energia cinética total do sistema formado pelos blocos e pela roldana nesse instante?
2. Qual é o módulo da velocidade dos blocos no instante em que o bloco menor se encontra a uma distancia vertical de em relação à sua altura original?
3. Na situação do item (b), qual é o módulo do momento angular da roldana em relação ao seu centro?
4. Quais são a aceleração dos blocos e a aceleração angular da roldana após o sistema ser liberado?

Letra (b):

Como o sistema é conservativo, a energia inicialmente armazenada na forma de energia potencial gravitacional é toda convertida em energia cinética. A energia inicial é , e depois a energia final é só a energia cinética (rotacional da roldana e translacional dos blocos):

Agora vou isolar do lado direito dessa expressão e jogar todas as outras quantidades para o outro:

Os valores das massas e do momento de inércia são os mesmos usados no passo anterior e a altura vale , então é só substituir:

Certo até aqui?

Letra (c):

O momento angular da roldana está relacionado com a velocidade linear final, saca só:

E usando a velocidade que acabamos de encontrar, fica tranquilo achar o momento angular:

Tranquilo até aqui? Vamos para o último item?

Letra (d):

Para resolver esse último item vamos relembrar de uma formula lá da cinemática:

A velocidade inicial é zero, a velocidade final é , o deslocamento foi de , daí fica tranquilo achar a aceleração linear:

E para achar a aceleração angular é só usar o raio:

Beleza?

Pronto pra próxima questão? =)