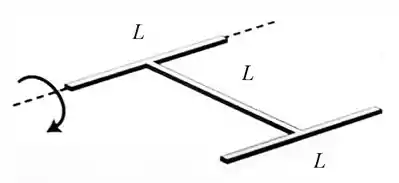
Um corpo rígido é formado por três barras finas de comprimento , unidas na forma de uma letra . O corpo pode girar livremente em torno de um eixo horizontal que coincide com uma das "pernas"do . O corpo é liberado a partir do repouso em uma posição em que o plano de está na horizontal. Qual é a velocidade angular do corpo quando o plano do está na vertical?
A.
B.
C.
D.
E.
Passo 1
Primeira coisa que a gente pode perceber é que só duas barras estão de fato girando. A barra 1 não contribui, porque o eixo tá passando por ela, então o momento angular dela é zero, e também ela não translada, então o CM dela tá paradinho.
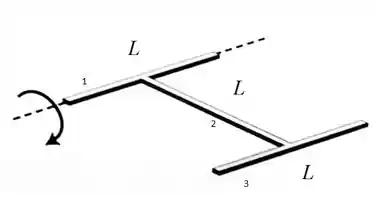
Já para as barras 2 e 3, temos que o centro de massa delas se movem. Olhando para o objeto formado pelas barras 2 e 3, temos que o centro de massa desse objeto está um pouco mais pra baixo do meio da barra vertical, que nem eu desenhei ali. Então, se a gente colocar a rigem bem na altura do centro de massa do nosso objeto na situação final, temos que, no inicio ele tava numa altura , e no final ele está numa latura zero.
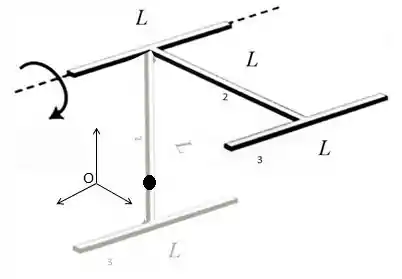
Beleza, como não temos forças dissipativas roubando energia do nosso sistema, temos que a energia mecânica se conserva.
Passo 2
Então:
Como o objeto parte do repouso:
Colocamos nossa origem de tal forma que a energia potencial final do objeto fosse zero . Ou seja, a origem está na altura do CM do nosso objeto.
O nosso objeto é formado por 2 barras. Vamos falar que cada barra tem massa . Então:
Passo 3
Vamos descobrir quem é o . Sabemos que ele é a posição do centro de massa do nosso objeto, então, usamos:
Esse é a distância dos centros de massa de cada barra ao eixo de rotação
Como
Então a posição do centro de massa é:
Logo,
Passo 4
Agora, vamos decobrir o
Maravilha, então o momento de inércia é:
O momento da barra que gira em torno de um eixo que passa pela sua extremidade vale
Já o momento da barra que está distante do eixo de , vale . Então:
Maravilha!
Passo 5
Agora é só voltar na equação do e substituir o que descobrimos:
Ajeitando isso daí:
Então:
Resposta
Alternativa B