Um aro de massa e raio é abandonado do repouso no topo de um plano inclinado simultaneamente com outro aro de massa e raio . Os aros rolam sem deslizamento. Qual aro chega primeiro à base do plano inclinado? Dado:
(A) O aro com massa maior.
(B) O aro com massa menor.
(C) O aro com maior momento de inércia.
(D) O aro com menor momento de inércia.
(E) Ambos chegam juntos.
Passo 1
Primeiramente vamos apontar as forças
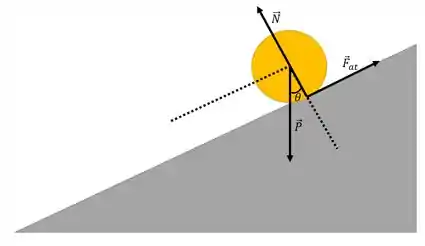
Temos que a única força que exerce torque sobre os aros é a força de atrito estático (já que os aros não deslizam). Esse torque é dado por
Passo 2
Como o aro não desliza temos que a aceleração angular se relaciona com a aceleração linear por
Assim
Passo 3
Já o aro não se move na direção perpendicular ao plano inclinado, temos que
E a força de atrito é dada por
Passo 4
Dessa forma a aceleração do bloco é dada por
Como o momento de inercia do aro é dada por
Temos
Ou seja, a aceleração do centro de massa do anel não depende nem de sua massa e nem do seu raio, assim os dois anéis têm a mesma aceleração linear e chegam ao mesmo tempo na base da rampa!
Resposta
(E)