Considere a equação diferencial ordinária
a) Obtenha a solução geral da equação utilizando o método das séries de potências ou de Frobenius.
b) Ache a solução do PVI dado pela equação com e .
c) Considere agora outro PVI, dado desta vez pela equação com e . Resolva este PVI no Mathematica (ou no Wolfram) e faça o gráfico de sua solução. Em seguida, determine os valores aproximados de para os quais a solução que você obteve neste item é tal que .
Passo 1
Fala galerinha, beleza? Bora resolver uma questão de EDO!
Nessa questão temos que considerar a equação diferencial
No item (a), ele pede para acharmos a solução geral da EDO usando o método de série de potências. Para isso, escrevemos a solução da equação como uma série
Os coeficientes são números reais. Derivando essa relação, achamos
Repare que agora soma começa em . Derivando novamente, encontramos
Passo 2
O próximo passo é substituir essas somas na equação:
Agora fazemos as distributivas:
Passo 3
O próximo passo é fazer uma mudança de variável nas somas para deixar todas elas com . Olhe para a primeira soma e defina . Com isso,
Assim,
Já na segunda soma, fazemos , de modo que
Com isso, a equação fica
Por fim, como a letra que usamos no índice de soma é irrelevante, podemos jogar fora o :
Para deixar todas as somas começando em , escrevemos
Com isso, podemos juntar as somas:
Como esse resultado deve valer para qualquer valor de , devemos ter
Desta forma, a solução geral da equação diferencial é
Passo 4
No item (b), queremos achar a solução da equação com as condições iniciais:
Lembre-se que, para , o único termo que sobrevive da série de potências é :
Já para a derivada, temos
Assim,
Vimos no último passo que . Logo, como , segue que . Agora olhemos para a relação de recorrência:
Substituindo nessa relação, achamos
Como , segue que
Agora fazemos :
Daí, usando , tiramos
Fazendo , você vai achar
Como , segue que
É fácil perceber que todos os seguintes serão nulos pois vão depender de e que são nulos. Logo, o único não nulo nesse PVI é
Com isso, a solução do PVI é
Repare que, de fato,
Além disso, essa função satisfaz a EDO!
Passo 5
No item (c), o problema pede para usarmos o software Mathematica para resolver a EDO com condições iniciais e . O Mathematica é um software pago, mas existe uma versão gratuita dele disponível na internet com algumas funções chamada Wolfram. A seguir dou o passo a passo de como você pode resolver esse problema por lá.
Primeiro entre no site wolframalpha.com. Em seguida, procure a opção “Differential equations” na primeira coluna de opções. Em seguida, clique na opção “specify initial values”. Daí, apague a equação escrita e escreva (x-1)*y’’-x*y’+y=0, y(0)=1, y’(0)=-2. É importante que você escreva exatamente dessa forma para o programa entender direitinho.
Fazendo isso, ele vai te dar a solução
Repare que e , de modo que . A seguir deixo o plot do gráfico que o programa forneceu:
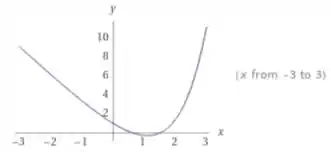
Fiz também um plot da função deixando em evidência suas raízes:
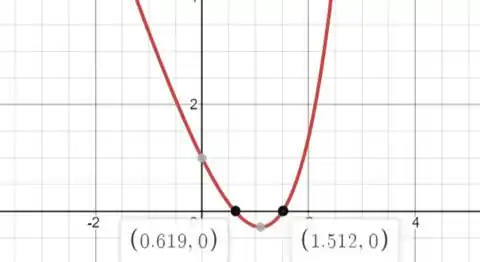
Vemos que para .
Ufa, deu bastante trabalho mas chegamos ao final do problema 😉!