USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 4 - Regra da Cadeia, Vetor Gradiente, Questão 2.1
2.1. Se , ache o vetor gradiente e use-o para achar a reta tangente à curva de nível de no ponto . Esboce a curva de nível, a reta tangente e o vetor gradiente.
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema queremos o vetor gradiente de no ponto e obter a reta tangente a .
Parece de boa? 😐
Um vetor gradiente de uma função é dado por
Já a reta tangente a um ponto a partir do gradiente é dado por
Já que e o vetor tangente a partir são perpendiculares.
Sacou? Bora lá! 😎
Passo 2
Se a função é dada por
Seu vetor gradiente é dado por
Assim, no ponto , temos
E como vimos no passo 1, a reta tangente a no ponto é dado por
Calculando o produto interno, vamos obter
Tranquilo até aqui? 😬
Passo 3
A curva de nível em é dada por
Esboçando essa elipse, a reta tangente e o vetor gradiente unitário, temos
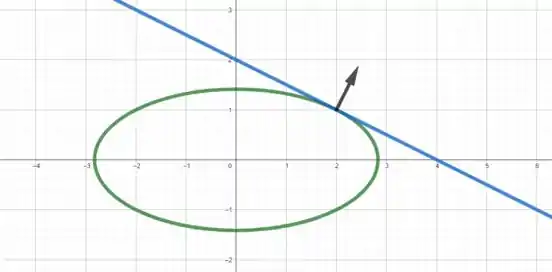
Sacou como faz? Responde Aí! 😉