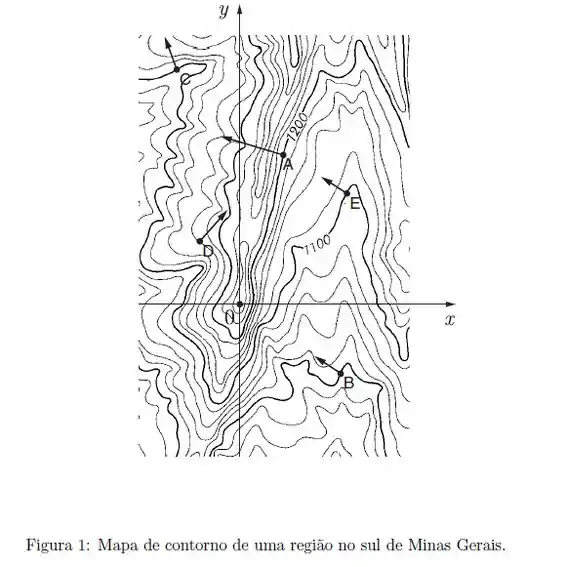
- Afigura mostra uma porção de um mapa da região Sul de Minas Gerais onde estão indicadas as curvas de nível da função altura com relação ao nível do mar. Existe uma linha grossa para cada de elevação e uma linha fina em cada intervalo de . Considere os pontos e no mapa. As setas indicam o vetor gradiente de no ponto indicado. Diga se as relações abaixo são verdadeiras ou não, marcando um “V” se a relação for verdadeira ou um “F” se a relação for falsa.
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
Passo 1
Vamos analisar :
Perceba que a linha grossa em que o ponto se encontra é a mesma que o ponto está. Portanto, .
Portanto a alternativa é falsa.
Passo 2
Verificar:
Da figura, percebemos que . Já vimos no passo anterior que , portanto a alternativa é verdadeira.
Passo 3
Analisar:
O vetor gradiente de é representado na figura. No ponto , o vetor gradiente tem componentes:
Agora perceba pela figura que no ponto , o vetor gradiente aponta para a esquerda, o que significa que a componente do vetor gradiente no ponto é negativa. Então: .
Logo a afirmativa é falsa.
Passo 4
Sabemos que
Perceba na figura que a componente do vetor gradiente no ponto é positiva pois o vetor aponta para cima. Logo
Alternatiiva verdadeira.
Passo 5
O vetor gradiente é dado por .
Pela figura, o vetor gradiente no ponto aponta para a esquerda. Então .
Item verdadeiro.
Passo 6
Perceba graficamente que o vetor gradiente no ponto aponta para cima. Logo, .
Falso.
Passo 7
Pela figura, é possível perceber que o vetor gradiente em aponta para a direita. Logo .
Verdadeiro
Passo 8
Graficamente, percebemos que o vetor gradiente no ponto aponta para a esquerda. Então .
Verdadeiro.
Passo 9
Primeiramente, perceba que os dois vetores gradientes, em e em , são negativos pois apontam para a esquerda.
Agora, note que o vetor gradiente em está mais inclinado, mais “deitado” do que o vetor gradiente em . Isso nos diz que a componente do vetor gradiente em é maior do que em , em módulo.
Porém como ambos são negativos, a componente do vetor gradiente em é maior do que em . Logo
Alternativa falsa.
Passo 10
Já vimos que em a componente do vetor gradiente é negativa, ou seja, . Além disso, vimos também que a componente do vetor gradiente em é positiva, ou seja, .
Logo:
Item falso.
Resposta
(F)
(V)
(F)
(V)
(V)
(F)
(V)
(V)
(F)
(F)