Considere a função .
(a) Indique a direção que determina a maior taxa de crescimento de no ponto . Qual é o valor dessa taxa?
(b) Calcule a derivada direcional de na direção no ponto .
(c) Considere a curva , , e a função composta . Calcule .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nessa questão, temos uma função onde
No item a) dessa questão, temos que indicar a direção onde a taxa de crescimento de é maior no ponto .
No item b) vamos obter a derivada direcional no mesmo ponto, mas na direção .
E no item c) vamos calcular a derivada de tal que onde .
E aí? Tem alguma ideia de como podemos fazer isso?? 🤔🤔
A derivada direcional de uma função nos mostra a a taxa de variação de uma função em uma certa direção, ou seja, os itens a) e b) vão ser obtidos pelo cálculo da derivada direcional.
Já o item c) pede para a gente calcular a derivada de uma função composta. Sabemos que a derivada de uma função composta é obtida pela regra da cadeia.
Entendeu? Bora começar!
Passo 2
A derivada direcional de uma função é sempre menor ou igual ao gradiente dessa mesma função, ou seja, o maior valor possível será quando a derivada direcional for igual ao seu gradiente.
Dessa forma, temos que calcular o gradiente de , substituir o ponto e obter seu módulo. Veja só!
O gradiente de uma função é dado por
Obtendo as derivadas parciais
Temos uma função composta aqui, então sua derivada é dada pela regra da cadeia (a derivada de dentro multiplicada pela derivada de fora) substituindo a função interna por uma variável qualquer na derivada de fora.
Substituindo por de volta
Agora obtendo a derivada parcial com relação a .
Também pela regra da cadeia, vamos obter
Com isso, nosso gradiente é dado por
Tranquilo até aqui? 😁
Passo 3
Como dito anteriormente, a direção onde mais cresce é a direção do vetor gradiente.
Então substituindo o ponto em , temos
Encontramos a direção, agora queremos saber a taxa de variação.
Então tiramos o módulo do vetor direcional
Logo, encontramos a taxa de variação como
Já no item b) vamos fazer algo parecido, porém na direção do vetor .
A primeira coisa a se fazer é escrever o vetor como um vetor unitário, pra isso dividimos ele pelo seu módulo
Agora calculamos o produto interno entre esse vetor e o gradiente de .
Interessante, não é? 😎
Passo 4
Por fim, vamos calcular a derivada de sendo que
Primeiro vamos escrever
Se
Substituindo em . e
Simplificando o expoente de , temos
Dessa forma, aplicando a regra da cadeia, temos
Substituindo por como solicitado no enunciado, temos
Encontramos o mesmo resultado da derivada direcional na direção . Perceba a semelhança
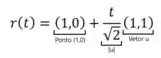
Encontramos uma outra forma de calcular a derivada direcional de uma função por equações paramétricas!
É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta
a) ,
b)
c)