Cálculo Aplicado – 1ª Atividade Avaliativa – 2021.1 – Prof. Thiago de Souza Pinto
Seja .
- Mostre que é conservativo
Passo 1
Vamos lá! O enunciado nos dá uma função vetorial e pede para a gente ver se isso é um campo conservativo... Eita! A gente tem que lembrar que se é um campo conservativo, então a gente tem que ter que o rotacional desse cara tem que ser igual ao vetor nulo
Para calcular o rotacional de alguém, a gente faz o determinante dessa matriz aqui
Agora a gente precisa só completar essa matriz com aqueles e ali. Esses caras são as componentes do nosso campo . Como a gente tem
Temos
Então a matriz que a gente tem que calcular o determinante é
Se der , o campo é conservativo, se não, não é!
Passo 2
Vamos calcular esse determinante doido aí. Como é uma matriz a gente usa a regra de Sarrus. A gente duplica as duas primeiras colunas
Primeiro a gente soma os produtos dessas diagonais que eu marquei aqui
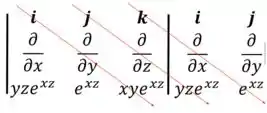
Isso vai nos dar
Passo 3
Agora a gente precisa calcular a soma dos produtos dos termos das diagonais que eu marquei aqui
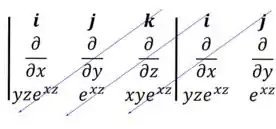
Isso nos dá
Passo 4
O determinante vai ser a subtração do nosso primeiro resultado com esse segundo
Como só devemos somar ou subtrair termos da mesma componente:
Logo
Então nosso campo é conservativo mesmo.