Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Vetor Gradiente

Ver Teoria
Exercício 55123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354565758596061626364656667686970717273747576

Enunciado

UFRJ. Cálculo 2. P1. 2022.1. Questão 2.

Seja f x , y = x + y x 2 + y 2 + 1 . Identifique e esboce todas as curvas de nível z = c . Para quais valores de c temos que a curva de nível correspondente é não vazia?

Passo 1

Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Foi dada uma função pra nós e o objetivo da questão é a gente identificar e esboçar as curvas de níveis não vazias de f x , y .

O que podemos fazer pra obter essas curvas? 🤔

A primeira coisa a se fazer é substituir f x , y por z , tal que

z = x + y x 2 + y 2 + 1

Analisando a função, é muito difícil de visualizar o intervalo onde z é definido, então podemos usar um método muito interessante que é obter os pontos máximos e mínimos de f e substituir na função para encontrar o intervalo de z .

Lembra como fazemos pra obter os valores máximos e mínimos de uma função?

Calculamos seu vetor gradiente e igualamos a 0 formando um sistema. A solução desse sistema é os pontos onde temos os pontos críticos.

Entendeu? Veja só! 😁

Passo 2

Calculando o gradiente de f , temos

∇ f = ∂ f ∂ x , ∂ f ∂ y

Derivando f em relação a x pela regra do quociente, temos

∂ f ∂ x = ∂ x + y ∂ x x 2 + y 2 + 1 - x + y ∂ x 2 + y 2 + 1 ∂ x x 2 + y 2 + 1 2

∂ f ∂ x = x 2 + y 2 + 1 - x + y 2 x x 2 + y 2 + 1 2

∂ f ∂ x = - x 2 + y 2 + 1 - 2 x y x 2 + y 2 + 1 2

Derivando f com relação a y pelo mesmo método, temos

∂ f ∂ y = ∂ x + y ∂ y x 2 + y 2 + 1 - x + y ∂ x 2 + y 2 + 1 ∂ y x 2 + y 2 + 1 2

∂ f ∂ y = x 2 + y 2 + 1 - x + y 2 y x 2 + y 2 + 1 2

∂ f ∂ y = x 2 - y 2 + 1 - 2 x y x 2 + y 2 + 1 2

Igualando esses dois resultados a 0 , vamos obter

- x 2 + y 2 + 1 - 2 x y x 2 + y 2 + 1 2 = 0 x 2 - y 2 + 1 - 2 x y x 2 + y 2 + 1 2 = 0

Como o denominador não influencia para o resultado dar 0 , então podemos desconsidera-lo

- x 2 + y 2 + 1 - 2 x y = 0 x 2 - y 2 + 1 - 2 x y = 0

Igualando as duas equações, temos

- x 2 + y 2 + 1 - 2 x y = x 2 - y 2 + 1 - 2 x y

x 2 = y 2

x = ± y

Tranquilo até aqui?

Passo 3

Substituindo essa informação em uma das equações do sistema, temos

- x 2 + x 2 + 1 - 2 x ( x ) = 0

1 - 2 x 2 = 0

Isolando x em um lado da igualdade, vamos obter

x = 1 2

Como x = ± y , então os possíveis pontos de máximos e mínimos de f será

P 1 = 1 2 , 1 2 ,   P 2 = 1 2 , - 1 2 ,   P 3 = - 1 2 , 1 2   e   P 4 = - 1 2 , - 1 2

Substituindo P 1 em f , temos

f 1 2 , 1 2 = 1 2 + 1 2 1 2 2 + 1 2 2 + 1 = 1 2

Substituindo P 2 em f

f 1 2 , - 1 2 = 1 2 - 1 2 1 2 2 + - 1 2 2 + 1 = 0

Já P 3 em f resultará em

f - 1 2 , 1 2 = - 1 2 + 1 2 - 1 2 2 + 1 2 2 + 1 = 0

Por fim, P 4 em f nos dá

f - 1 2 , - 1 2 = - 1 2 - 1 2 - 1 2 2 + 1 2 2 + 1 = - 1 2

Interessante, não é?

Passo 4

Com os resultados obtidos anteriormente, vemos que o máximo valor para z é 1 2 e o menor valor para z é - 1 2 .

Como o denominador de f nunca vai a 0 , então a função f é definida em todo o intervalo 1 2 , - 1 2 .

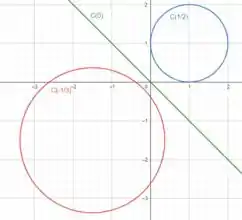
Vamos esboçar três curvas de níveis c . Para c = 0 , c = 1 / 2 e c = - 1 / 3

Em c = 0 , temos

0 = x + y x 2 + y 2 + 1

x = - y

Em c = 1 / 2

1 2 = x + y x 2 + y 2 + 1

x 2 + y 2 + 1 = 2 x + 2 y

x - 1 2 + y - 1 2 = 1

Em c = - 1 / 3

- 1 3 = x + y x 2 + y 2 + 1

x 2 + y 2 + 1 = - 3 x - 3 y

x + 3 2 2 + y + 3 2 2 = 7 2

Plotando essas curvas no plano x y , temos as curvas de níveis

É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta

z = 1 2 , - 1 2

Exercícios de Livros Relacionados

a ) Determine o gradiente de f b ) Calcule o gradiente no ponto P c ) Determine a taxa de variação de f em P na direção do vetor u . f x , y , z = x + y z P 1,3 , 1 u = 2 7 , 3 7, 6 7
Determinar o vetor gradiente das funções dadas nos pontos indicados:c) z = s e n( 3 x + y ) ; P 0 , π 2
Determinar o vetor gradiente das funções dadas nos pontos indicados:g) f u ,v ,w = u 2 + v 2 - w 2 + u v w ; P 0,1 ,0
Determine a equação da reta tangente à curva de nível dada, no ponto dado. x 2 + x y + y 2 - 3 y = 1 ,e m 1,2
Determine a função f : R 2 → R cujo gráfico passa pelo ponto ( 1,2 , 1 ) e tal que ∇ f x , y = ( 2 x y 3 - 2 x , 3 x 2 y 2 + 2 y - 1 )