Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Vetor Gradiente

Ver Teoria
Exercício 63123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616264656667686970717273747576

Enunciado

P2 – Cálculo Diferencial e Integral 2 – 2021.2 – Profª Cláudia Brunosi Medeiros

Um reservatório cilíndrico fechado deve conter x litros de fluido, onde x é o número formado pelos últimos três dígitos do seu RA. Determine as dimensões do depósito de modo que a quantidade de material usada em sua construção seja mínima e determine qual é a área mínima.

Passo 1

Este é um exercício de otimização para funções de várias variáveis. Pelo enunciado a gente tem que encontrar alguma função e o vínculo ao qual o nosso problema está sujeito.

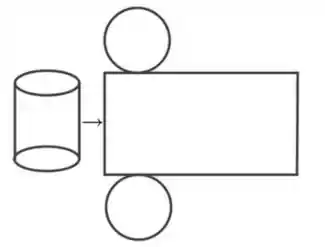
O problema nos fala que o reservatório tem formato cilíndrico, olhando a imagem aqui de cima a gente já sabe como obter sua área e seu volume

Á r e a c i l i n d r o = á r e a   l a t e r a l + 2 × á r e a   d a   b a s e V o l u m e c i l i n d r o = á r e a   d a   b a s e   × a l t u r a

Para transformar isso em funções, vamos usar chamar de r o raio do cilindro e h sua altura. Então a gente pode escrever

Á r e a = 2   π r h + 2 π r 2 V o l u m e = π r 2 h  

As funções são essas, mas cadê o vínculo?! Bem, o vínculo vem sempre como uma restrição. No nosso caso, a gente tem que ter o volume do cilindro sendo aquele valor x que tem a ver com o nosso registro. No caso, eu vou usar x = 123 mas ele podia ser qualquer outro valor dependendo do seu registro. Então temos

π r 2 h   = 123

A gente sempre tenta escrever a restrição como

g x , y = 0

Então temos

g r , h = π r 2 h - 123 = 0

Como a função que queremos minimizar é a área, escrevemos

f r , h =   2   π r h + 2 π r 2

Passo 2

Para minimizar a nossa função f ( r , h ) vamos usar o método dos multiplicadores de Lagrange

∇ f r , h = λ ∇ g r , h

Vamos calcular esses gradientes aí

∇ f r , h = f r ,   f h   e   ∇ g r , h = g r ,   g h

Como f r = 2   π h + 4   π r f h = 2   π r g r =   2   π r h g h = π r 2

Temos os gradientes

∇ f r , h = 2 π h + 4   π r ,   2 π r ∇ g r , h = ( 2 π r h ,   π r 2 )

Dessa maneira temos

∇ f r , h = λ ∇ g r , h 2 π h + 4   π r ,   2 π r = λ 2 π r h ,   π r 2 = ( λ 2 π r h ,   λ π r 2 )

Onde obtemos o sistema

2 π h + 4   π r =   λ 2 π r h   2 π r = λ π r 2

Esse sistema pode ser simplificado para

h + 2 r =   λ r h   2 = λ r

Passo 3

Agora a gente precisa encontrar o multiplicador λ . Da última igualdade do sistema que a gente montou temos 2 = λ r

λ = 2 r   Substituindo o valor de λ   que encontramos na primeira equação do sistema temos

h + 2 r = 2 r r h h + 2 r = 2 h

h = 2 r

Encontramos uma relação entre a altura e o raio para o nosso problema. Se usarmos essa relação na nossa restrição

π r 2 h = 123 π r 2 2   r = 2   π r 3 = 123 r 3 = 123 2   π ≈ 19,6 r =   19,6 3 = 2,7

E encontramos o valor do raio do nosso cilindro. Então teremos a altura como

h = 2 .   2,7 = 5,4

Esses são os valores que minimizam a nossa área.

Passo 4

Para calcular a área mínima, usamos os valores do raio e da altura que obtemos

r = 2,7   e   h = 5,4

Na expressão da área

Á r e a =   2   π r h + 2 π r 2 = 2 . π .   2,7 . 5,4 + 2 . π . 2,7 2

Á r e a = 91,6 + 45,8 = 137,4   u . a .  

Resposta

Raio = 2,7 u.c.Altura = 5,4 u.c. Área mínima = 137,4 u.a.

Exercícios de Livros Relacionados

a ) Determine o gradiente de f b ) Calcule o gradiente no ponto P c ) Determine a taxa de variação de f em P na direção do vetor u . f x , y , z = x + y z P 1,3 , 1 u = 2 7 , 3 7, 6 7
Determinar o vetor gradiente das funções dadas nos pontos indicados:c) z = s e n( 3 x + y ) ; P 0 , π 2
Determinar o vetor gradiente das funções dadas nos pontos indicados:g) f u ,v ,w = u 2 + v 2 - w 2 + u v w ; P 0,1 ,0
Determine a equação da reta tangente à curva de nível dada, no ponto dado. x 2 + x y + y 2 - 3 y = 1 ,e m 1,2
Determine a função f : R 2 → R cujo gráfico passa pelo ponto ( 1,2 , 1 ) e tal que ∇ f x , y = ( 2 x y 3 - 2 x , 3 x 2 y 2 + 2 y - 1 )