UFF, Sem Campus, Cálculo IIB, P1 - Prof. Jorge Delgado - 2023 - Verão, Questão 3b.
3 – Considere a função .
b) Calcule e desenhe os vetores gradientes nos pontos e . Use o mesmo desenho do item anterior.
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse item estamos interessados em obter os vetores gradientes de nos pontos e .
Lembra como fazemos isso? 👀
Um vetor gradiente é um vetor normal à superfície e é composto pelas derivadas parciais de
Substituindo o ponto no vetor, obtemos o vetor normal que queremos
Entendeu? Bora começar! 😉
Passo 2
Primeiro vamos obter as derivadas parciais
Pelo método de derivação polinomial...
Agora para a outra derivada...
Portanto, o vetor gradiente é dado por
Tudo certo até aqui? 👍
Passo 3
Agora obtemos o vetor em si substituindo as coordenadas do ponto no vetor.
Para o ponto
Esse vetor é normal a , tem como origem o ponto e tem tamanho em e em .
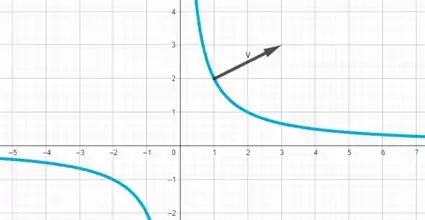
Para o ponto
Já esse vetor é dado por
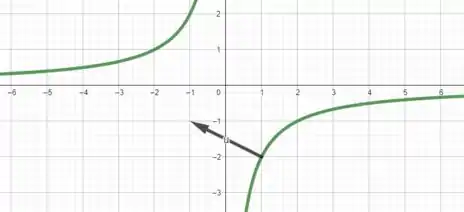
É isso! Essa resolução te ajudou? Responde Aí! ✌
