- Achar o volume do sólido limitado superiormente pela esfera, inferiormente pelo plano e lateralmente pelo cilindro .
Passo 1
Pow! O problema nos pediu um volume de sólido, e a essa altura, podemos calcular um volume utilizando uma...
Mas veja que para resolver essa integral aí necessitamos de algumas informações:
- Quem é o ?
- Quem é a região de integração ?
- Quem é o ?
- Quem é a região de integração ?
Para ambas as perguntas, vamos encontrar as respostas no esboço do sólido no espaço. Bora?
Passo 2
Pois bem! O sólido que estamos trabalhando está delimitado pela esfera
Essa é uma esfera normal e de raio :
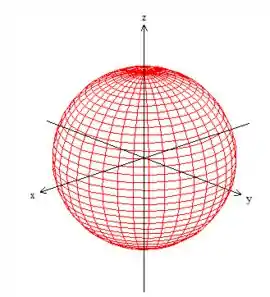
Mas não queremos toda a esfera, por isso o problema nos limita a esfera pelo plano , ou melhor, o próprio plano
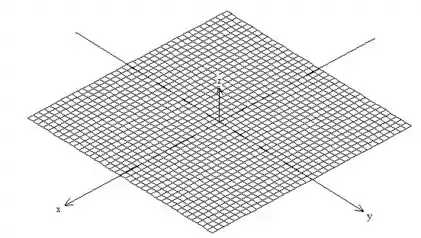
Além disso, lateralmente existe um cilindro de raio
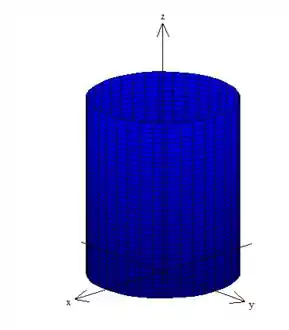
que corta o sólido.
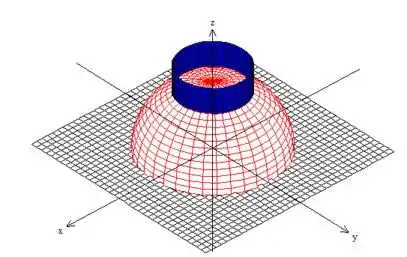
É como se fosse esse cortador aqui

Sacou? E o sólido é justamente esse do interior deste cilindro:
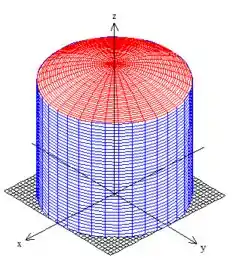
Passo 3
Agora já conseguimos juntos aqui responder a primeira pergunta:
Afinal de contas você já sabe que essa função aí é a função que representa a superfície “teto” do sólido, certo?
E quem é essa superfície?
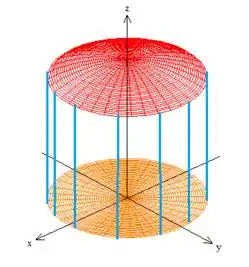
Exato! O pedacinho de esfera ;)
Como a esfera tem essa equação aqui , precisamos mexer um pouquinho nela a transformando nessa função de e , bastando isolar o no caso...
como o teto esta em cima...
Passo 4
Quanto a essa pergunta aqui...
como e são as variáveis principais, devemos encontrar essa região na “sombra” do sólido no plano .
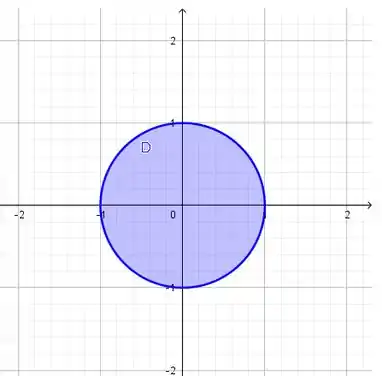
Essa sombra, ou melhor, projeção, é circular e delimitada pelo cilindro que no plano nos dá essa circunferência
As variáveis e estão dentro desse circulo aqui
Passo 5
Pow! Estamos trabalhando com uma região circular... ou seja... vamos utilizar as coordenadas polares:
Uma equação que nos ajuda muito é a equação da circunferência...
E, claro, o Jacobiano:
Para encontrar os limites de e , basta que olhemos novamente para a região
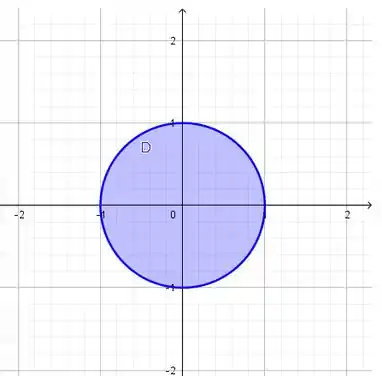
para que possamos notar que varia de até o raio da circunferência azul
e dá uma volta completa:
Passo 6
Nessa mudança é fundamental não se esquecer de trocar a função que estamos trabalhando pelas novas coordenadas:
substituindo...
não se esqueça de multiplicar pelo , heim!
Logo essa é a função que estamos trabalhando agora
Passo 7
Montando a integral, agora, com todos os dois dados principais:
Resolvendo primeiro a integral de dentro...
Pow! Essa integral de dentro aí pode ser resolvida caso façamos uma troca:
antes de substituirmos, não esqueça de trocar os limites também
esse menos aí dentro some se invertemos esses limites de dentro
integrando...
integrando a última...