Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes por Integrais Duplas

Ver Teoria
Exercício 301234567891011121314151617181920212223242526272829313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990

Enunciado

Integral Dupla sobre regiões mais gerais

Considere a região espacial

U = x , y , z ∈ R 3   0 ≤ z ≤ 2 x + y ,     x + y ≤ 1 ,     x ≥ 0 ,     y ≥ 0  

b) Calcule o volume de U

Passo 1

O sólido U tem a limitação em z , ou seja ele é o volume entre a função z = 2 x + y e o plano x y . Vimos na teoria que esse volume vai ser

V U = ∬ R 2 x + y d x d y

Com R sendo a região da base desse sólido.

Vamos ver como é o gráfico dessa base

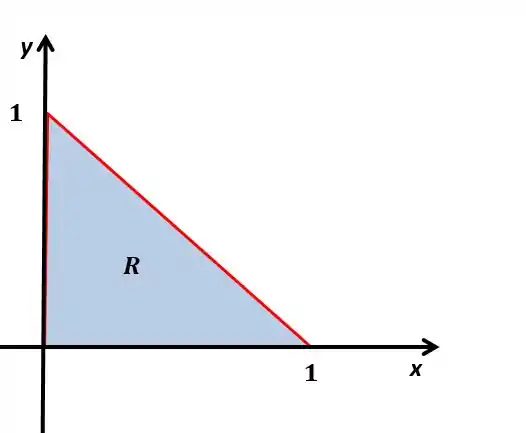
Neste caso, podemos fazer essa região sendo do tipo I ou do tipo II, tanto faz. Vamos fazer uma região do tipo I

Para isso vamos ter

R = { x , y | a ≤ x ≤ b ,   g 1 x ≤ y ≤ g 2 x }

Conseguimos ver que x vai de 0 à 1 , enquanto y vai de 0 à reta, a reta vai ser

x + y = 1

y = 1 - x

A região vai ficar

R = { x , y | 0 ≤ x ≤ 1 ,   0 ≤ y ≤ 1 - x }

Passo 2

A integral vai ficar

V U = ∫ 0 1 ∫ 0 1 - x 2 x + y d y d x = ∫ 0 1 ∫ 0 1 - x 2 x 2 y d y d x

Vamos ver como fazer a integral de

∫ 2 y d y

Vamos lembrar que 2 x = e x ln ⁡ 2 , a integral fica

∫ e y ln ⁡ 2 d y

Fazendo u = y ln ⁡ 2 , vamos achar sua derivada

d u = ln ⁡ 2 d y

d y = d u ln ⁡ 2

A integral fica

∫ e y ln ⁡ 2 d y = ∫ e u d u ln ⁡ 2 = 1 ln ⁡ 2 ∫ e u d u = e u ln ⁡ 2

Voltando para y vamos ter

e u ln ⁡ 2 = e y ln ⁡ 2 ln ⁡ 2

Usando as propriedades de log

e y ln ⁡ 2 ln ⁡ 2 = 2 y ln ⁡ 2

Passo 3

Voltando para a integral

∫ 0 1 2 x 2 x ln ⁡ 2 0 1 - x d x = ∫ 0 1 2 x 2 1 - x ln ⁡ 2 - 2 0 ln ⁡ 2 d x = ∫ 0 1 2.2 x 2 - x ln ⁡ 2 - 2 x ln ⁡ 2 d x

⇒ ∫ 0 1 2 ln ⁡ 2 - 2 x ln ⁡ 2 d x = 1 ln ⁡ 2 ∫ 0 1 2 - 2 x d x = 1 ln ⁡ 2 2 x - 2 x ln ⁡ 2 x = 0 1

⇒ 1 ln ⁡ 2 2.1 - 2 1 ln ⁡ 2 - 2.0 - 2 0 ln ⁡ 2 = 1 ln ⁡ 2 2 - 2 ln ⁡ 2 - - 1 ln ⁡ 2

⇒ 1 ln ⁡ 2 2 - 2 ln ⁡ 2 + 1 ln ⁡ 2 = 1 ln ⁡ 2 2 - 1 ln ⁡ 2 = 2 ln ⁡ 2 - 1 ln 2 ⁡ 2

Resposta

  1. V U = 2 ln ⁡ 2 - 1 ln 2 ⁡ 2

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais expressando a área em termos de uma integral simples e usando uma calculadora para estimar a integral.A parte da superfície z = 1 /
Use um sistema de computação algébrico para determinar o volume exato do sólido.Delimitado por z = x 2 + y 2 e z = 2 y .
Utilize coordenadas polares para determinar o volume do sólido dado.Limitado pelo paraboloide z = 1 + 2 x 2 + 2 y 2 e pelo plano z = 7 no primeiro octante
Desenhe o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 4 - x - 2 y d x d y
Nos Exercícios 67 e 68, esboce a região de integração e o sólido cujo volume seja dado pela integral dupla.