Considere o sólido limitado pelo paraboloide e pelos planos e.
- Escreva a integral que fornece o volume sólido.
- Determine o volume do sólido.
Passo 1
Bom, essa questão é bem direta naquilo que quer. Pra a gente saber resolver, é bom sabermos
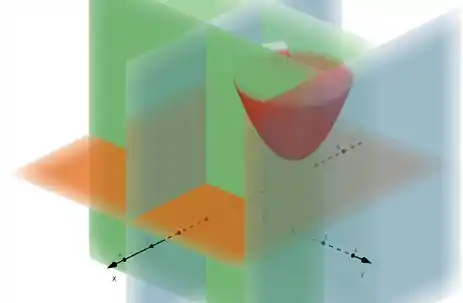
A vista superior nos ajuda a perceber como o paraboloide está confinado entre os planos.
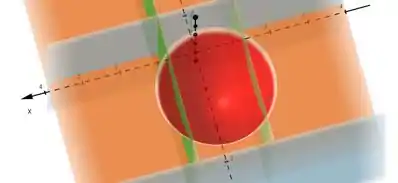
Passo 2
Sabendo agora nossa região, é só ter a sagacidade de ver que o sólido procurado tá limitado pelo paraboloide e pelos planos destacados.
Passo 3
- Como a integral dupla calcula o volume de tudo oque está abaixo da função até o plano xy, temos que tirar o volume que está abaixo do eixo !
- Assim ficamos com uma diferença de duas integrais. A gente obtém ele pelo volume abaixo do paraboloide, menos o volume que esta abaixo do , dentro da região do retângulo que x e y fazem.
- Com variando de -1 a 1, e de 0 a 4.
Então a gente fica com a integral como?
A primeira é o volume de tudo abaixo do paraboloide, entre os planos. A segunda é o volume abaixo do plano , que nós não queremos.
Passo 4
(b) Então agora a gente resolve e corre pra nota 10!
Um monte de integral tranquila, né? Agora é so aplicar os intervalos de volta e show!