Considere a região do plano tal que , onde
Seja , onde
- Desenhe e desenho ao lado o interior de (pontilhando) e a fronteira de .
- Seja a integral dupla
- Seja
Escreva como uma soma de duas integrais iteradas, integrando primeiramente com respeito a e em seguida com respeito a .
Calcule , usando a ordem de integração que preferir.
Onde é a região dada no enunciado inicial. Calcule o volume de
Passo 1
Letra a)
Vamos lá galera, a questão aqui pede pra gente esboçar essa região, que na verdade é a união de duas regiões, vamos fazer cada uma de uma vez! Além disso, ele quer que a gente desenhe a mesma região só que com o contorno pontilhado e depois somente a fronteira. Já que a prova pede, quem somos nós pra dizer não, né? Vamos fazer os três esboços.
Entendendo a região , essa função não parece muito simples né? Vamos elevar ao cubo dos dois lados, fica assim
Que já é um pouco mais conhecida! Perceba que, em só queremos o intervalo de , nosso esboço é esse então
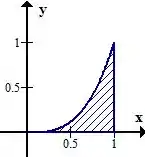
Passo 2
A região é levemente diferente, primeiro porque os valores de são negativos, perceba que ele varia de . Além disso, é a raiz negativa de :
Se elevarmos ao cubo dos dois lados o sinal de menos não desaparece! Fica assim
Temos a mesma função de , só que negativa! Como esboçamos isso? É só refletir a região pra baixo do eixo x, olha só
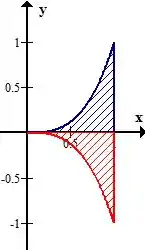
Pronto! Resolvido o problema! Agora ele pede pra gente desenhar a mesma função só que com a fronteira pontilhada para representar somente o interior de . Seu pedido é uma ordem! Fica assim
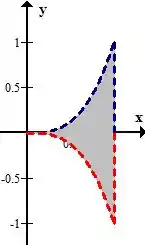
E agora somente a fronteira de
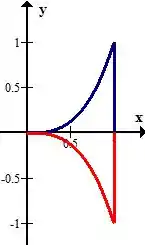
Passo 3
Letra b)
Aqui ele pede pra gente escrever a integral dupla da função dentro dessa região que acabamos de esboçar, certo? Note que ele pede pra gente escrever como uma soma de duas integrais, seria isso aqui
Ou seja, precisamos de duas regiões que, juntas, dê exatamente a região . Só que, percebe que já é descrita como a união de e , portanto podemos reescrever essas integrais assim
Ótimo, os limites de e já são descritos no enunciado, só precisamos coloca-los nas integrais e substituir por , lembre que vamos escrever a integral primeiro em e depois em , portanto os limites da integral de fora estão associados a e de dentro a , assim olha
:
:
Juntado as duas integrais
Passo 4
A segunda parte da letra b pede pra gente calcular essa integral ai na ordem que quiser, né? Se a gente tentar integrar da forma que está escrito a gente não consegue nem sair do lugar! Integrar em relação à é simplesmente impossível, como vamos fazer isso então?
Po, quando a gente tem que fazer uma integral assim e não conseguimos, já vimos que podemos tentar inverter a ordem de integração! E como fazemos isso? Temos que voltar ao esboço e encontrar os novos limites, dá uma olhada aqui
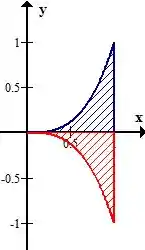
Nossa região é tudo isso ai, já reescrevemos esses limites de cima e de baixo em função de , lembra? Ficou assim
Perceba que, em toda região, sempre está limitado em baixo por e em cima por ! Ou seja, dá pra gente juntar as duas regiões em uma só com esses limites aqui
Passo 5
Vamos reescrever a integral e resolvê-la
Agora da pra integrar em
Pra integrar isso ai vamos ter que fazer uma substituição
Perceba que podemos escrever como , certo? Então
Voltando para a integral, os novos limites vão ser
Lembre-se que pode ser escrito como , com isso, multiplicando por fica
Passo 6
Letra c)
Aqui ele pede pra gente calcular o volume de , sendo que essa região é limitada em pela mesma região que acabamos de trabalhar, então isso deve facilitar nossas contas.
Sabemos que o volume de um sólido limitado por e por uma função pode ser dado pela integral dupla
Nesse caso o domínio é a região que já delimitamos e a função que limita é , que já integramos também na letra b! Portanto, o volume dessa função pode ser dado por
Resposta
a)
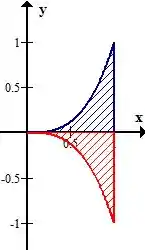
b)
c)