4) Esboce o sólido cujo volume é dado pela integral
Justifique o seu raciocínio.
Passo 1
Falaaaa... Belezinha???
Nessa questão vamos esboçar o volume da integral dada.
Mas você pode estar se perguntando: Ueee.. mas integral dupla não é área??
Então... Vamos fazer um paralelo com integral simples. Lembra quando a gente queria calcular a área entre duas curvas, e , que a gente calculava a integral:
A gente pode pensar de forma semelhante pra integral duplas. Pra calcular o volume entre duas curvas, e usamos:
Passo 2
Como vamos esboçar o volume, então vamos ter um gráfico em três dimensões, certo?
Maaaas pra ficar mais fácil de ver como vai ficar, vamos usar a estratégia de fazer primeiro os gráficos em duas dimensões.
Para temos a região delimitada, que aparece colado no sinal da integral. Essa região é a projeção da curva no plano . Como se fosse a sombra da curva com e variando entre 0 e 1.
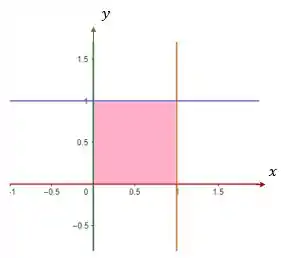
Passo 3
Para o plano , nós temos . Então varia de 0 a 1 e varia de 0 a Como , então temos variando de 0 a .
Repara que é uma parábola com a concavidade pra baixo. Então teremos:
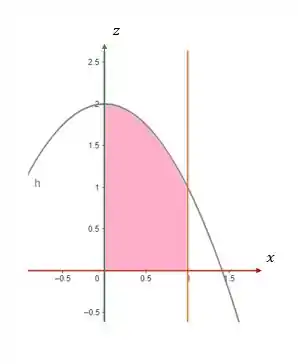
E para o plano vamos ter uma parada beeem análoga a essa.
Esboçando o sólido, então:
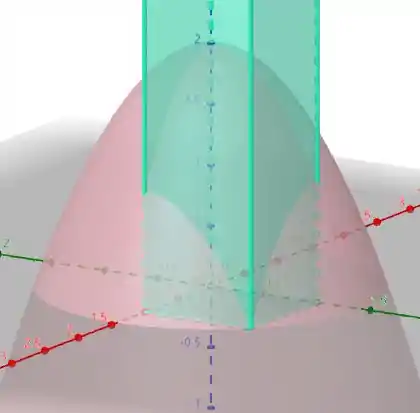
Resposta
Imagem nos passos.