Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes por Integrais Duplas

Ver Teoria
Exercício 241234567891011121314151617181920212223252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990

Enunciado

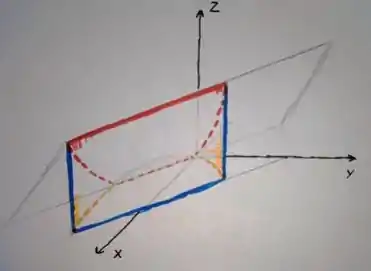
Questão3: Seja E a região R 3 limitada pelos planos z = 0 , x + y = 2 e - 2 x - 2 y + z = 0 , e o cilindro parabólico x - y 2 = 0 .

  1. Faça um esboço de E .
  2. Calcule o volume de E .

Passo 1

a )

Bem, para o esboço de E , eu sugiro que você vá desenhando uma a uma superfície, até terminar e ver o sólido. Como esse sólido é complicado de desenhar no computador, eu fiz a mão livre, veja:

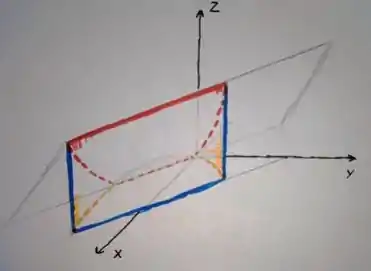
Esse é o sólido E , e repara que eu o desenhei da seguinte forma:

  1. Primeiro coloquei o os eixos coordenados x ,   y e z .
  2. Em seguida, eu fiz a reta x + y = 2 em azul no chão.
  3. Continuando no chão, eu fiz a parábola x = y 2 , em laranja.
  4. Depois eu fiz a reta vermelha tracejada no chão também y = - x , já que representa a intercessão do plano z = 2 x + 2 y (em vermelho) com o chão z = 0 .

    5. OBS: Veja que eu fiz com que a reta tracejada vermelha, “cortasse” a parábola em dois pontos. Isso acontece porque matematicamente, a reta y = - x e a parábola x = y 2 , têm dois pontos em comum: 0,0   e   1 ,   - 1 .

  5. Depois disso eu fiz o resto do plano vermelho, puxando a reta tracejada vermelha.
  6. Então por último, subi as paredes azul e laranja (a azul é a parede formada pelo plano x + y = 2 e a laranja, é a parede formada pelo paraboloide x = y 2 .

Sacou???

Passo 2

b )

Com o sólido desenhado, podemos calcular o volume dele! Se o problema quer volume, a essa altura do campeonato, então o que ele realmente quer é que calculemos uma integral dupla:

V o l u m e   E = ∬ R   f x ,   y - g x ,   y   d A

O que precisamos encontrar aqui é quem é essa f x ,   y , g x ,   y e quem é o R . Bora?

Passo 3

Bem, a função f x ,   y é sempre a função que delimita superiormente o sólido, enquanto a g x ,   y é a função de baixo. Se olharmos novamente para o nosso sólido:

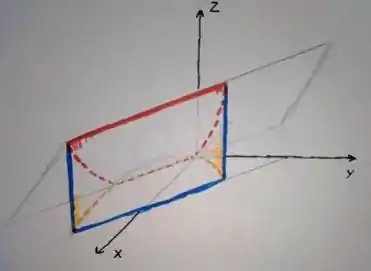
Conseguimos ver que quem está delimitando por cima é o plano vermelho, enquanto que quem delimita por baixo é o z = 0 . Como a equação do plano vermelho é:

z = 2 x + 2 y

Já temos a nossa função f x ,   y ...

f x ,   y = z = 2 x + 2 y

A função g x ,   y = z = 0 (O chão do sólido).

Passo 4

Agora nos falta encontrar quem é R !

Bem, R é sempre a região de integração. Se o nosso volume está sendo integrado em x e y , então o nosso R é a projeção do sólido E no plano x y ...

Veja que essa basicamente é a região de integração no plano x y . Vou trazê-la de forma mais fácil de trabalhar aqui:

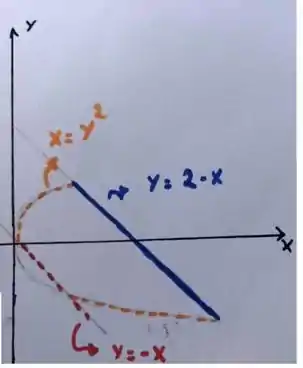
Então, o que temos que fazer, basicamente é descrever essa região! Bora?

Passo 5

Para descrever essa região, primeiro eu quero que você entenda que existe um ponto, e esse ponto é x = 1 , em que a nossa região se separa em 2 :

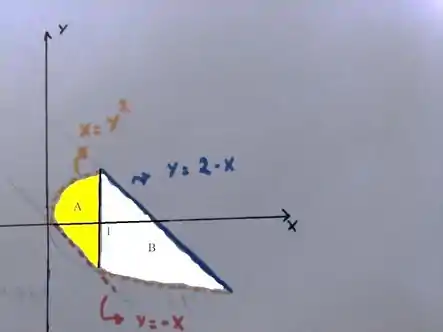
Por que x = 1 separa essas duas regiões? A justificativa está aqui oh:

Assim, podemos descrever a região R , como a união de duas outras regiões:

R = A ∪ B

Passo 6

A região A a gente pode descrever como do tipo 2 onde o x varia em um intervalo numérico bem definido:

0 ≤ x ≤ 1

Enquanto o y varia de uma base a um teto:

B a s e   v e r m e l h a ≤ y ≤ T e t o   L a r a n j a

A base vermelha é a reta y = - x enquanto o teto...

x = y 2         o u           y = x

Então...

- x ≤ y ≤ x

Passo 7

Já a região B ...

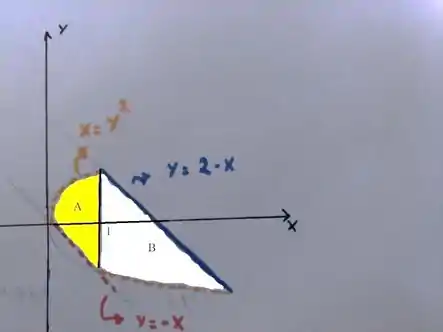
Bem, podemos descrevê-la também como do Tipo 2 , onde o x varia de 1 até o último x que é dado no encontro entre a reta azul e a parábola laranja:

y = 2 - x       o n d e         x = y 2 …

y = 2 - y 2     →           r e s o l v e n d o   p o r   b á s k a r a       y = - 2

Então x = 4 . Logo x varia de 1 a 4 , nessa região...

1 ≤ x ≤ 4

Enquanto o y varia da parábola, ao teto da reta azul:

- x ≤ y ≤ 2 - x

Passo 8

Agora não tem por onde correr! É só montar a integral e partir para o abraço!

V o l u m e   E = ∬ R   f x ,   y - g x ,   y   d A   →

V o l u m e   E = ∬ R   2 x + 2 y   d A   →

Já que R = A ∪ B ...

V o l u m e   E = ∬ A   2 x + 2 y   d A + ∬ B   2 x + 2 y   d A

Como

A :     0 ≤ x ≤ 1 - x ≤ y ≤ x                               B :     1 ≤ x ≤ 4 - x ≤ y ≤ 2 - x

Então...

V o l u m e   E = ∫ 0 1 ∫ - x x 2 x + 2 y d y   d x + ∫ 1 4 ∫ - x 2 - x 2 x + 2 y d y   d x

Passo 9

Vamos calcular a primeira integral então...

∫ 0 1 ∫ - x x 2 x + 2 y d y   d x = ∫ 0 1 ∫ - x x 2 x + 2 y d y   d x =

∫ 0 1   2 x y + y 2   - x x d x = ∫ 0 1 2 x x + x 2 - 2 x - x + - x 2 d x =

∫ 0 1 2 x 3 2 + x + x 2 d x = 4 x 5 2 5 + x 2 2 + x 3 3 0 1 =

4 5 + 1 2 + 1 3 = 24 + 15 + 10 30 = 49 30

Passo 10

Partindo para a segunda integral agora:

∫ 1 4 ∫ - x 2 - x 2 x + 2 y d y   d x = ∫ 1 4 ∫ - x 2 - x 2 x + 2 y d y   d x =

∫ 1 4   2 x y + y 2   - x 2 - x d x = ∫ 1 4 2 x 2 - x + 2 - x 2 - 2 x - x + - x 2 d x =

∫ 1 4 4 x - 2 x 2 + 4 - 4 x + x 2 - - 2 x 3 2 + x d x = ∫ 1 4 - x 2 + 4 + 2 x 3 2 - x d x =

- x 3 3 + 4 x + 4 x 5 2 5 - x 2 2 1 4 = - 4 3 3 + 16 + 4 2 2 5 2 5 - 4 2 2 - - 1 3 + 4 + 4 5 - 1 2 =

- 64 3 + 16 + 4 ⋅ 32 5 - 16 2 - - 1 3 + 4 + 4 5 - 1 2 =

- 63 3 + 4 + 124 5 + 1 2 = - 630 + 120 + 744 + 15 30 =

249 30

Passo 11

Então...

V o l u m e   E = ∫ 0 1 ∫ - x x 2 x + 2 y d y   d x + ∫ 1 4 ∫ - x 2 - x 2 x + 2 y d y   d x

V o l u m e   E = 49 30 + 249 30 = 298 30 =

149 15

Resposta

a )

b ) 149 15

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais expressando a área em termos de uma integral simples e usando uma calculadora para estimar a integral.A parte da superfície z = 1 /
Use um sistema de computação algébrico para determinar o volume exato do sólido.Delimitado por z = x 2 + y 2 e z = 2 y .
Utilize coordenadas polares para determinar o volume do sólido dado.Limitado pelo paraboloide z = 1 + 2 x 2 + 2 y 2 e pelo plano z = 7 no primeiro octante
Desenhe o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 4 - x - 2 y d x d y
Nos Exercícios 67 e 68, esboce a região de integração e o sólido cujo volume seja dado pela integral dupla.