UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 9a.
9 - Calcule o volume dos sólidos delimitados pelas superfícies dadas:
a) , e
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nessa questão, temos que calcular o volume de um solido limitado pelas equações , e .
E agora? Entendeu alguma coisa? 👀
Em outras palavras, vamos observar as equações que limitam nossa região e aplicar o método de integração para calcular o volume.
Podemos observar que e são os limites da altura do nosso sólido e são os limites das laterais. Analisando as equações, vemos que estamos lidando com circunferências e hiperboloide então vamos usar coordenadas polares para resolver essa questão.
Bora ver como é nosso solido?
Passo 2
Se plotarmos as curvas, temos
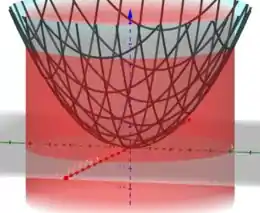
Temos algo como se fosse uma tigela de base cilíndrica, consegue ver?
Quando temos uma questão de volume com integrais polares, temos a seguinte integral para resolver
Onde é a maior curva em e a menor. Já , , e são os valores de e da integral polar que já sabemos obter.
A equação limita nossa região de integração, dela podemos tirar que varia de a e de a .
Com isso, nossa integral é dada como
Convertendo nossa função de integração para e ou no caso . Lembrando que não podemos esquecer do jacobiano que já está inserido (destacado em vermelho).
Agora podemos iniciar nossos cálculos! bora lá! 😁
Passo 3
Primeiro integramos com relação a pelo método de integração polinomial onde dividimos a variável pela sua potência e somamos no seu expoente.
Aplicando os limites de integração
Agora com base nesse resultado, integramos com relação a
Como nossa função de integração é uma constante, sabemos que a integral de uma constante é a própria constante multiplicada pela variável de integração
Aplicando os limites de integração
Com isso, o volume descrito por aquelas equações é de
É isso! Essa resolução te ajudou? Responde Aí! ✌
