UFPE, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº Ricardo F. da Silva - Undécima Lista, Questão 5b
Use uma integral dupla para calcular a área das seguintes regiões. Faça um esboço da região.
a) A região no primeiro quadrante limitada por e .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular a área da região entre as curvas e . Vamos começar fazendo o esboço da região, pra gente entender como é essa área.
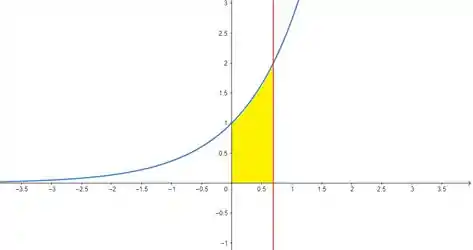
Como ele quer apenas no primeiro quadrante, nossa região vai ser essa em amarelo. Repare que nossa região é limitada horizontalmente pelo eixo () e pela reta . E a região é limitada verticalmente pelo eixo () até a curva , certo? Então, esses vão ser nossos limites de integração.
A fórmula do cálculo de área usando integral dupla é dada por:
Onde é a nossa região de integração.
Vamos lá!
Passo 2
No passo , nós vimos que nossos intervalos de integração serão:
Assim, temos a integral de área:
Integrando primeiro em relação a , temos:
Aplicando os limites de integração em :
Integrando agora em relação a , vamos ter:
Aplicando os limites de integração em :
Como a função exponencial é a inversa do logaritmo natural, temos que . E qualquer número elevado a é igual a . Então:
E temos nossa área:
Valeu, galera! Até a próxima! 😉