UFPE, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº Ricardo F. da Silva - Undécima Lista, Questão 4c
Determine o volume do sólido dado.
c) Abaixo da superfície e acima do triângulo de vértices , e .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume gerado pela região abaixo da superfície e acima do triângulo de vértices , e . Nós sabemos que o volume é definido através da integral dupla:
Nesse caso, a nossa região é dada pelo triângulo:
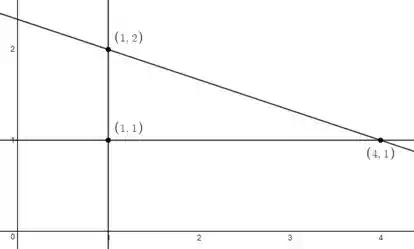
Mas para definir a região precisamos saber quem é essa reta que passa entre os pontos e . Nós podemos fazer isso calculando a inclinação da reta por meio de e substituindo na equação geral da reta:
Assim, definimos os intervalos de integração em e em e calculamos nossa integral dupla para obter o volume.
Vamos lá!
Passo 2
Usando os pontos e , vamos calcular a inclinação da reta:
Substituindo na equação geral da reta, temos:
Então podemos escrever nossa região da seguinte forma:
Passo 3
Então, o volume do solido que é restrito abaixo de na região é dado por:
Agora vamos integrar, primeiro em :
Aplicando os limites de integração:
Agora integramos em relação a :
Aplicamos os limites de integração:
E temos nosso volume:
Valeu, galera! Até a próxima! 😉