UFSCAR, Sem Campus, Cálculo 3, Listas de C3 - Profª Alessandra Verri - Lista 1, Questão 6a
Esboce o sólido cujo volume é dado pela integral
(a)
Passo 1
Eaew, belezinha?
Temos que determinar o esboço do sólido cujo volume é dado pela integral
Então, temos que a altura desse sólido é dada pela função que está sendo integrada. E os limites desse sólido em x e y, são dados pelos limites de integração
Então vamos lá!
Passo 2
Temos que a altura do sólido é dada por:
Temos também que
.
Passo 3
Agora, com essas informações, podemos fazer o esboço do sólido:
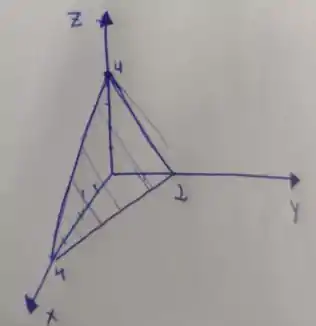
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
No decorrer da questão.