Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes por Integrais Duplas

Ver Teoria
Exercício 331234567891011121314151617181920212223242526272829303132343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990

Enunciado

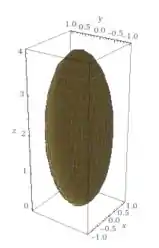
  1. Identifique e desenhe a superfície S ⊂ R 3 , dada abaixo:

    2. S = x , y , z ∈ R 3 |   4 z - z 2 = 4 ( x 2 + y 2 ) .

  2. Considere a região U ⊂ R 3 , dada por:

S = x , y , z ∈ R 3 |   4 z - z 2 - 4 x 2 - 4 y 2 ≥ 0 ,   z ≥ 2

  1. Desenhe a fronteira de U .
  2. Escreva o volume de U na forma de V o l U = ∫ a b f r d r , determinando a ,   b e f .
  3. Calcule o volume de U .

Passo 1

a) Nossa! Do jeito que essa superfície está, não dá para trabalhar! Então vamos comigo tentar coloca-la de uma forma mais elegante?

A dica é justamente a gente tentar completar quadrado no primeiro lado da equação para sumir com esse termo 4 z .

Multiplicando ambos os lados da equação por - 1 temos e somando 4 nos dois lados...

4 z - z 2 = 4 x 2 + y 2 →   z 2 - 4 z = - 4 x 2 + y 2   →     z 2 - 4 z + 4 = - 4 x 2 + y 2 + 4

Observamos que o primeiro termo da igualdade pode ser reescrito como

( z - 2 ) 2 = 4 ( - x 2 - y 2 + 1 )

Passando o 4 do segundo membro dividindo e passando os termos x e y também para primeiro termo ganharemos por fim

z - 2 2 4 = - x 2 - y 2 + 1     →       x 2 + y 2 + z - 2 2 4 = 1

Veja como nós simplificamos a nossa visualização da equação :)! Essa coisa linda representa pra gente um elipsoide deslocado no eixo z pra cima, dessa forma aqui:

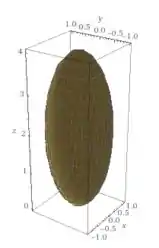
Passo 2

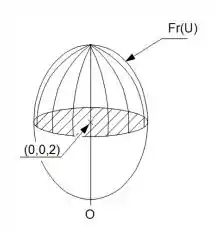
Letra b) item i: Podemos perceber que o sólido é a mesmo, porém queremos a parte acima do plano z = 2 que corta o nosso volume justamente no centro do elipsoide

A fronteira, é justamente essa casca de cima:

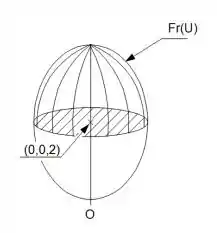
Passo 3

Item ii - Lembre-se que encontrar o volume sobre um determinado gráfico e acima de um plano z = 2 é a mesma coisa que encontrar o resultado da integral ∬ R ( z x , y - 2 ) d x d y . Devido a isso, é legal a gente começar a ver a nossa superfície em função de z , dessa forma:

( z - 2 ) 2 = 4 - x 2 - y 2 + 1   →   z - 2 = 2 1 - x 2 - y 2     →     z = 2 1 - ( x 2 + y 2 ) + 2

Observe que pegamos a parte positiva quando extraímos a raiz, pois o exercício nos pede a parte de cima do nosso elipsoide

Porém, o exercício nos pede para deixar algo em função de r , e onde vamos encontrar esse r ? Na mudança para coordenadas cilíndricas:)

x = r . c o s ⁡ ( θ ) y = r . s i n ⁡ ( θ ) J = r x 2 + y 2 = r 2

Passo 4

Agora vamos identificar os limites das novas variáveis.

Pra encontrar quais são os limites de r , vamos olhar para a intercessão do plano z = 2 com o nosso elipsoide

x 2 + y 2 + z - 2 2 4 = 1 z = 2   →   x 2 + y 2 + 2 - 2 2 4 = 1   →   x 2 + y 2 = 1

Comparando o resultado da intercessão com a equação x 2 + y 2 = r 2 , identificamos que

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

Passo 5

Pronto! Agora a gente pode juntar tudo e resolver o item da questão!

Substituindo na nossa integral as nossas coordenadas e os seus limites, a gente ganhará... Ahhh!!! Não esqueça do produto pelo jacobiano, heim!

V o l u m e = ∬ R ( z - 2 ) d x d y = ∬ R 2 1 - ( x 2 + y 2 ) + 2 - 2 d x d y →

∫ 0 1 ∫ 0 2 π 2 1 - r 2 .   r d θ d r

Resolvendo a integral de dentro...

V o l = ∫ 0 1 ∫ 0 2 π 2 1 - r 2 .   r d θ d r = ∫ 0 1 2 r 1 - r 2 . θ 0 2 π d r =

E substituindo os nossos limites em θ

= ∫ 0 1 4 π r 1 - r 2 d r

Logo, a = 0 ,   b = 1 e f r = 4 π r 1 - r 2

Passo 6

Item iii - Resolvendo a integral de fora por substituição u = 1 - r 2 e d u = - 2 r d r e não esquecendo de mudar os limites de u quando r = 0   e   r = 1 , ganharemos como volume...

V o l = ∫ 0 1 4 π r 1 - r 2 d r = - 2 π ∫ 1 0 u   d u = - 2 π   2 u 3 2 3 1 0 = 4 π 3

Resposta

a )

b )   i :

i i : a = 0 b = 1 f r = 4 π r 1 - r 2

i i i : V = 4 π 3

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais expressando a área em termos de uma integral simples e usando uma calculadora para estimar a integral.A parte da superfície z = 1 /
Use um sistema de computação algébrico para determinar o volume exato do sólido.Delimitado por z = x 2 + y 2 e z = 2 y .
Utilize coordenadas polares para determinar o volume do sólido dado.Limitado pelo paraboloide z = 1 + 2 x 2 + 2 y 2 e pelo plano z = 7 no primeiro octante
Desenhe o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 4 - x - 2 y d x d y
Nos Exercícios 67 e 68, esboce a região de integração e o sólido cujo volume seja dado pela integral dupla.