UFPE, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº Ricardo F. da Silva - Undécima Lista, Questão 4d
Determine o volume do sólido dado.
d) Limitado pelo cilindro e pelos planos , , no primeiro octante.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume limitado pelo cilindro e pelos planos , , no primeiro octante. Nós sabemos que o volume é definido através da integral dupla:
Onde a função . E a região está no plano (ou ). Assim, devemos integrar a função no domínio de integração limitado pela circunferência no plano :
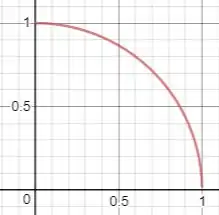
Assim, vamos calcular o volume através da integral dupla:
Vamos lá!
Passo 2
Vamos começar integrando em relação a :
Aplicando os limites de integração:
Agora integrando em relação a , temos:
E aplicando os limites de integração em :
Temos nosso volume:
Valeu, galera! Até a próxima! 😉
Resposta
Exercícios de Livros Relacionados
Encontre a área da superfície com precisão de quatro casas decimais expressando a área em termos de uma integral simples e usando uma calculadora para estimar a integral.A parte da superfície z = 1 /
Use um sistema de computação algébrico para determinar o volume exato do sólido.Delimitado por z = x 2 + y 2 e z = 2 y .
Utilize coordenadas polares para determinar o volume do sólido dado.Limitado pelo paraboloide z = 1 + 2 x 2 + 2 y 2 e pelo plano z = 7 no primeiro octante
Desenhe o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 4 - x - 2 y d x d y
Nos Exercícios 67 e 68, esboce a região de integração e o sólido cujo volume seja dado pela integral dupla.