UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, AV3 - 2022.1
Calcule o volume do solido limitado pelos paraboloides
Passo 1
Com a ajuda do nosso querido GeoGebra iremos visualizar o solido que iremos calcular o volume
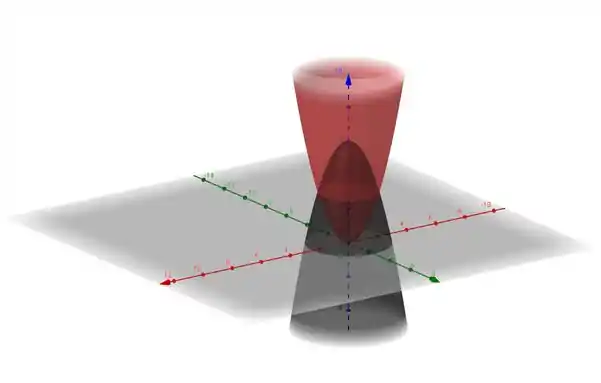
Para se calcular o volume de um solido por meio de integração, a relação que usamos é
Passo 2
Como o solido possui simetria em relação ao eixo z e as equações que o limitam tem termos quadráticos, vamos usar coordenadas cilíndricas.
Vamos agora encontrar os intervalos de integração. Substituindo nossa parametrização:
Para o outro paraboloide:
Então agora sabemos que os valores de z variam entre . Pelo próprio desenho gerado, sabemos que o ângulo varia entre A última variação que precisamos encontrar é do nosso querido r.
Para isso, iremos realizar a igualdade entre as duas paraboloides, e assim encontrar o valor máximo de r.
Passo 3
Agora finalmente podemos montar e começar a resolver nossa integral:
E aqui terminamos nossa questão, espero que tenham aprendido um pouco mais hoje. Forte abraço e até uma próxima.