Considere a quádrica
a) Desenhe-a e identifique a sua interseção com os seguintes planos:
- , para e
b) Considere a região espacial
Escreva a fronteira de usando igualdades ou desigualdades.
c) Seja
Escreva o volume na forma
explicitando e .
d) Calcule o volume de .
e) Calcule o volume de .
Passo 1
Vamos fazer ao contrário? É exatamente esse o processo que fazemos para descobrir de qual quádrica estamos tratando!
Vamos lá então, para ver a interseção da superfície com o plano , pegamos sua equação e trocamos por ;)
E aí está! Temos e , mas com um sinal de menos entre eles. Então temos uma hipérbole no plano com as bocas abertas (:O) na direção (ele está com o sinal positivo):
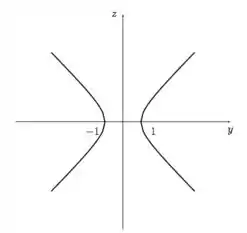
Passo 2
Agora, vejamos a interseção com o plano , pelo mesmo processo:
E veja só! Mais uma hipérbole, igualzinha à outra, exceto pelo fato de agora termos no lugar de . Estamos, então, no plano , com as bocas abertas no sentido :
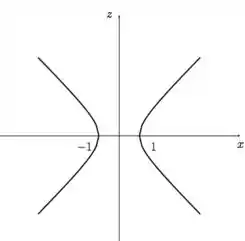
Passo 3
Vamos lá, agora vejamos as curvas de nível para , e :
Supondo , temos:
E teríamos uma circunferência de raio , exatamente na origem, no plano !
E, agora, veja comigo, se ou , pouco importa! Porque está ao quadrado! E, como e o estão ambos com sinal de “menos” na frente, quando passarmos para o lado direito da equação, não há perigo de ficar negativo! Assim, não teremos nunca pontos de indeterminação independentemente do que coloquemos. Fica:
Ou seja, temos círculos de raio ! Veja o esboço aqui em baixo:
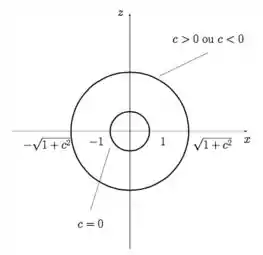
Passo 4
Agora, podemos descobrir qual é a quádrica que estamos procurando! Veja, temos hipérboles nos plano e . E, quando fatiamos a quádrica por plano paralelos ao , com , independentemente de qual coloquemos, sempre temos circunferências! Juntando todas as peças, temos nas mãos um hiperboloide de uma folha!! Olha ele aí:

Passo 5
b) Ok, vamos por partes. Primeiro, vamos ver a desigualdade da esquerda,
Temos, então, que
E chegamos exatamente no hiperboloide do item ! Percebe? Agora a única diferença é essa desigualdade... O que ela significa? Que estamos fora dele, pois, colocando o dedo sobre sua superfície, para um dado raio , temos que é maior ou igual a esse raio!
Passo 6
Show, agora, vamos para o lado direito da desigualdade:
Já está pronto, né? Se tivéssemos um sinal de igual, seria um cilindro de raio , certo? Mas a inequação nos diz que, colocando o dedo sobre o cilindro, andamos com ele para dentro, pois é menor ou igual ao raio! Assim, essa inequação representa a parte interna do cilindro!
Passo 7
Beleza, prossigamos! Já podemos resolver a questão. Vimos que a região está fora do hiperboloide, mas dentro do cilindro. Logo, sua fronteira é contida pela união de cada uma dessas superfícies!
Agora, temos que expressar isso que acabamos de dizer com equações e inequações! As equações já temos, e são as próprias equações do hiperboloide e do cilindro. Mas, pense comigo: se colocarmos as duas equações não estaremos definindo fronteira nenhuma, pois essas duas superfícies tem “área infinita”, sem nenhuma restrição! Assim, temos que descobrir onde o hiperboloide e o cilindro de interceptam, e dizer que a fronteira está restrita entre a primeira interseção e a segunda ;) Aqui vai um esboço do que estamos falando:

Para ver essas interseções, basta substituir uma equação na outra! Colocando o do cilindro na equação (com sinal de “igual” mesmo—é superfície, não região) do hiperbolóide, temos:
Opa! Olha que resultado lindo! Descobrimos que as alturas dessas circunferências de interseção ocorrem em e ! Logo, ! Essa exatamente a inequação que estava faltando! É ela que define o limite das equações da fronteira de ! Portanto, temos, para o cilindro:
E, para o hiperboloide:
E, por fim, dizemos que a fronteira de é , ou seja, a união das superfícies, ambas restritas com entre e ;)
Passo 8
c) Legal, já vimos que o a região é aquela que está fora do hiperboloide, mas dentro do cilindro. Agora, temos que fazer sua interseção com o semi-espaço , ou seja, tudo acima do plano ! Esboçando a situação, temos:
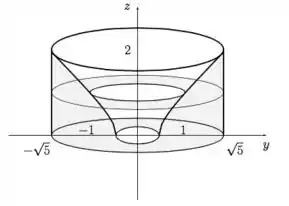
E agora? Como fazemos para definir o volume dessa região com integrais duplas? Basta definirmos a função a ser integrada e a região de integração!
Olhando para o esboço, vemos que a função é a altura, , dada pela equação do hiperboloide. E a região de integração é a projeção do hiperboloide no plano , que é o anel de raio interno , do hiperboloide, e externo , do cilindro!
Então, a integral fica:
Em que é o domínio em anel: , ou seja, o conjunto dos pontos que satisfazem círculos de raios variando entre e . E vem da equação do hiperboloide:
Portanto, o volume é:
Passo 9
d) Calculemos o volume do passo anterior! Para isso, temos que escolher a substituição correta. A dica é: domínio em disco, fatia ou anel? Use coordenadas polares! Neste caso, pela própria definição que demos à região , temos o raio variando entre e , e, como é o anel completo, o varia entre e ! Portanto, como estamos integrando agora entre duas constantes, podemos escolher a ordem de integração :D
Não esquecendo do jacobiano, igual a , e nem que, em coordenadas polares , o volume fica:
Agora, temos que pensar em qual é a primitiva de . Veja, como temos que a derivada de é , então, provavelmente essa expressão veio da regra da cadeia. Por exemplo, derivando , temos:
Viu só? Estamos quase chegando nela! Para “consertar” esse que apareceu aí, vamos dividir a expressão por ! Dividir por uma constante não afetará nas derivadas, e ela será carregada até o final! Fica, então:
Integrando em relação à , temos simplesmente entre e :
Passo 10
e) Ufa! Finalmente, último item a cumprir! E olha que maravilha, ele pede o volume de ! E quem é ? É duas vezes o volume de ! Lembra como obtivemos ? Foi pegando o e dizendo: queremos apenas a parte que tem . Agora, estamos dizendo: queremos tudo, e ! Como é simétrico em relação ao plano , então o valor desse volume é o dobro do calculado no passo anterior ;)
Resposta
a) Quádrica: Hiperboloide de uma folha:
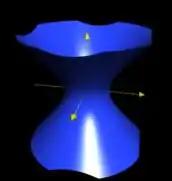
Interseções com e com são hipérboles, e com , para qualquer , são circunferências.
b) e
c)
d)
e)