UFU, Sem Campus, Cálculo 2, Listas de C2 - Profª Ana Paula - Lista 7 - Integrais Duplas, Questão 9b
Determine o volume do sólido dado
b) Abaixo da superfície e acima do triângulo com vértices em e .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcular o volume do sólido abaixo da superfície e acima do triângulo com vértices em e .
Para isso, primeiramente devemos analisar a região :
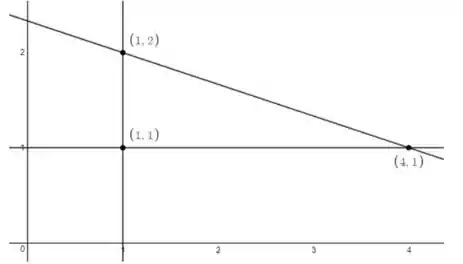
Vamos descobrir através da inclinação dessa reta!
Logo, a reta é dada por:
Dessa forma, podemos escrever a nossa região assim:
Passo 2
Temos então que o volume do sólido que é restrito abaixo de na região é dado por:
Integrando com relação a :
Agora, integrando com relação a :
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Encontre a área da superfície com precisão de quatro casas decimais expressando a área em termos de uma integral simples e usando uma calculadora para estimar a integral.A parte da superfície z = 1 /
Use um sistema de computação algébrico para determinar o volume exato do sólido.Delimitado por z = x 2 + y 2 e z = 2 y .
Utilize coordenadas polares para determinar o volume do sólido dado.Limitado pelo paraboloide z = 1 + 2 x 2 + 2 y 2 e pelo plano z = 7 no primeiro octante
Desenhe o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 4 - x - 2 y d x d y
Nos Exercícios 67 e 68, esboce a região de integração e o sólido cujo volume seja dado pela integral dupla.