Considere a região espacial
- Identifique a fronteira da região plana
- Escreva a fronteira de como uma união de superfícies , determinando cada uma delas através de desigualdades ou igualdades. Esboce a fronteira de
- Calcule o volume do sólido , onde
- Descreva, através de desigualdades ou igualdades, a parte da fronteira de que está contida no plano
Como uma cônica clássica, ou seja, determine sua equação e seu nome.
Passo 1
a) Vamos lá! A fronteira de é uma superfície, e é o plano A interseção dos dois nos vai dar uma curva, certo? É desta cônica que o enunciado está falando ;)
Ok, e como a encontramos? Simplesmente trocando os sinais de e de por sinais de para termos uma superfície, e colocando ! Se você perceber, tanto para a inequação do lado direito, como para a do lado esquerdo, colocando , teremos:
E que curva é essa? É uma elipse! Tenha sempre em mente: Se temos e somados, pode ser uma elipse ou circunferência. Se os denominadores deles forem diferentes, é uma elipse!
Isso acontece pois, na verdade, tanto como são paraboloides simétricos um ao outro em relação à . Quando formos esboçá-los mais a frente, ficará mais claro, mas, por enquanto, apenas trabalhemos na teoria, fazendo a interseção das superfícies com o plano e vendo que dá a mesma curva!
Passo 2
b) A fronteira de é a casca do volume , certo? Então, para pegar essa superfície, trocamos esses sinais de “maior/menor que” por sinais de igual, e teremos as seguintes superfícies:
Beleza, agora podemos ver quem é cada uma ;)
Passo 3
A maneira mais rápida de esboçar qualquer superfície, é zerar cada uma das variáveis e observar a projeção no plano formado pelas outras duas. Por exemplo, para a , se zerarmos a variável , teremos, no plano :
Que é uma parábola com a boca aberta para o sentido positivo do eixo , deslocada em também no eixo !
Da mesma forma, zerando a variável , teremos:
E essa é uma parábola, exatamente como a outra, mas dessa vez no plano ! Assim, fica fácil de ver que temos um paraboloide elíptico! Por que elíptico? Porque no plano , ou seja, em , que fizemos no passo anterior, vimos que a projeção era uma elípse!
Aqui vai seu esboço:
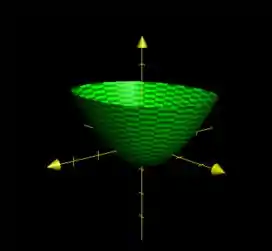
Passo 4
Vamos para a outra agora:
O processo é exatamente o mesmo! Vamos, para essa superfície, zerar a componente ? Teremos:
Agora temos uma parábola, no plano , com a boca virar no sentido negativo do eixo , e deslocada em no sentido positivo desse eixo!
Show, agora, vamos zerar a variável :
E temos outra parábola (de novo!!), com a boca no sentido negativo do eixo , e deslocada em no sentido positivo!
Percebe que temos o mesmo paraboloide que do passo anterior, mas agora apontando para baixo? Olha ele aqui:
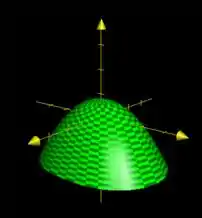
Passo 5
Beleza, temos uma superfície, temos outra... e aí? Agora só temos que fazer a união das duas! Veja, como elas cortam o plano na mesma elipse, aquela do passo 1, temos uma casca fechada certinho :D
Enfim, juntando os dois paraboloides, teremos:
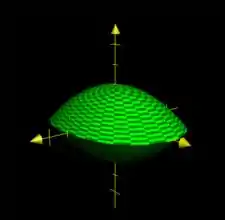
Essa aí é “fronteira de ”. E, apenas para efeitos de resposta formal, podemos defini-la assim:
Ou seja, o conjunto dos pontos pertencentes ao , tais que respeitam a equação de cada paraboloide, sendo que, os da têm coordenada , e da tem coordenada ;)
Passo 6
c) Essa interseção do enunciado nada mais é do que a parte do volume que temos quando percorremos de a no eixo , e de a no eixo ! Assim, para saber o volume, a função que devemos integrar é o elipsoide de cima menos o de baixo!
Teremos, então:
Perceba que o elipsoide de cima, é o que tem a boa para baixo, e o de baixo é o que tem a boca para cima!
Desenvolvendo, temos:
Tirando a constante pra fora,
Resolvendo a integral de dentro,
Agora, resolvendo a integral em relação a ,
Eis aí o volume! unidades de volume :D
Passo 7
d) Queremos agora a fatia de para quando , certo? Bom, como essa é a única restrição que estamos aplicando em , tudo o que temos que fazer é pegar a definição de e fazer !
Mas como definimos ? é o volume com as restrições de e !
Assim:
Agora, basta colocar :
E pronto! Temos essa fronteira de definida para :D
Resposta
a)
b) ;
c)
d)