Calcule o volume do sólido delimitado pelo gráfico de:
Passo 1
Antes de tudo, vamos desenhar essa região para entender melhor o problema. Temos um plano , um cilindro de base parabólica e um plano .
Para o cilindro, é uma boa você desenhar a parábola no plano e depois repeti-la ao longo do eixo (afinal, a coordenada não está presente na equação, o que significa que ela vale para qualquer ). Para o plano , fazemos o mesmo, desenhamos a reta no plano e a repetimos ao longo do eixo . O outro plano, , já é mais chatinho de desenhar, mas como isso aqui é só um esboço, você pode desenhar um plano qualquer, é só para termos uma noção da região mesmo.
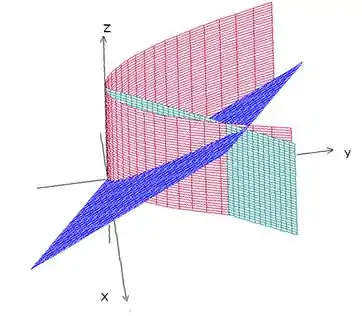
No plano , a região é limitada pelo cilindro e pelo plano verde e na coordenada , limitada pelo plano azul. Como não há mais informações para limitar a coordenada , vamos assumir que , para continuarmos o problema.
Nossa região é então a que está entre as superfícies vermelha e verde e abaixo do plano azul:
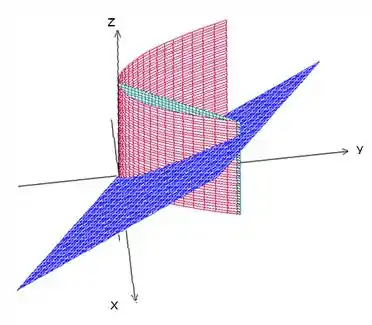
Chamando de essa região que acabamos de analisar, o problema pede então .
Passo 2
Beleza, agora precisamos escrever matematicamente essa região. Como podemos ver, na coordenada ela está limitada pela equação do plano azul e pelo plano , enquanto no plano ela é limitada pela seguinte àrea:
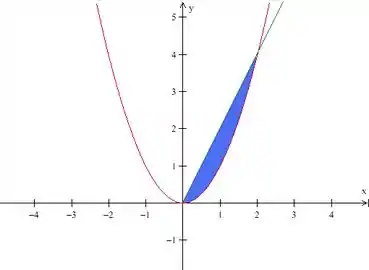
Essa seria a região vista de cima, percebeu? O plano verde virou uma reta e o cilindro de parábola virou uma parábola . Certo, então vamos escrever o seguinte:
Onde é essa área que acabamos de ver acima.
Passo 3
Agora precisamos escrever matematicamente essa área, como em qualquer integral dupla que já fizemos.
Vamos enxergar essa área como região do tipo I, limitada na coordenada por funções (a equação da parábola e da reta) e em por números.
Como em a área está entre a equação da parábola e a da reta, temos que:
Agora vamos ver a coordenada . Pela figura, vemos que varia desde a origem até o encontro da reta com a parábola, que acontece em (para ver isso, basta substituir uma equação na outra). Então temos:
Beleza, então vamos escrever essa área assim:
Passo 4
Agora vamos substituir na integral esses intervalos que encontramos:
Cuidado com a ordem dos diferenciais! Ela tem que acompanhar os intervalos da integrais.
Passo 5
Agora em relação a :
Passo 6
Finalmente, em relação a :