Seja , onde é o disco fechado de raio centrado no ponto e é o semiplano fechado
- Esboce a região plana e determine-a através de desigualdades em coordenadas polares e
- Usando coordenadas polares, escreva a integral dupla
- Escreva o volume do sólido em função de (sendo a integral do item anterior), onde
Na forma
Explicitando as constante e e a função
Obs.: Neste item não é pedido o cálculo da integral
Passo 1
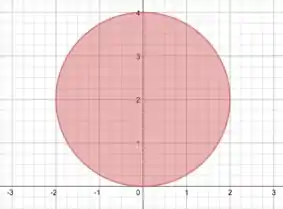
a) Vamos lá! Comecemos visualizando esse disco!
Sabemos que a equação de um disco centrado na origem com raio é , show? Para transladar essa bolota no eixo , basta colocarmos, em vez de , ! Se não lembra disso, veja a equação geral da circunferência:
no caso da nossa, temos o :) E a equação do disco fica:
Aqui vai uma figura pra ajudar:
Passo 2
Beleza, e agora? Vamos fazer a interseção desse disco com o semiplano? Como ele é , então temos que preencher tudo o que estiver no primeiro e quarto quadrantes! Fica assim:
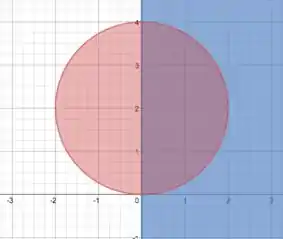
Show? E a interseção é a parte que está tanto no disco como no semiplano, em roxo :D
Passo 3
Bem, ainda não parametrizamos a região, né? Mas aqui o caminho é simples: tudo o que temos que fazer é parametrizar o disco, e depois restringir os parâmetros para apenas a parte do primeiro quadrante, consegue visualizar?
Sabemos que a equação do disco é:
Usando coordenadas polares, temos e , tendo como o ângulo com o eixo e a distância da origem. Quanto ao jacobiano da mudança polar, lembre, é !
Então, colocando a parametrização na equação do disco, temos:
como o termo entre parêntesis é sempre ,
Show! Agora já sabemos de quanto a quanto nosso raio varia! E lembrando que como está no primeiro quadrante, varia entre e !
Passo 4
b) Partiu montar a integral! Como a função que estamos integrando é simplesmente , então no lugar dela colocamos . Lembrando, ainda, que o jacobiano vale ,
Lembrando que no passo anterior vimos que ! Prosseguindo, temos:
E aí está! , e ;)
Passo 5
c) Show! Para calcular volumes com integrais duplas, temos que integrar a função num determinado domínio, certo? No caso, é a função , e o domínio é o mesmo de sempre (a tal interseção do disco com o semiplano). Lembrando que esse que coloquei aí desnecessariamente é apenas para lembrar que o domínio fosse entre e a , teríamos que fazer essa diferença!
Temos, assim:
E podemos separar em duas integrais!
A integral da esquerda, já temos, que é a nossa .
A outra, é a integral dupla de uma constante, ou seja, uma área! E que área é essa? Da região ! Essa, por sua vez, é metade da área de um disco de raio , ou seja,
Então, o volume fica sendo:
Resposta
a) 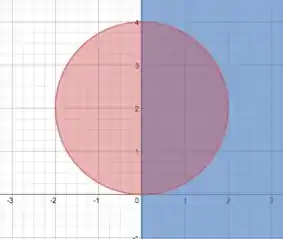
b)
c)