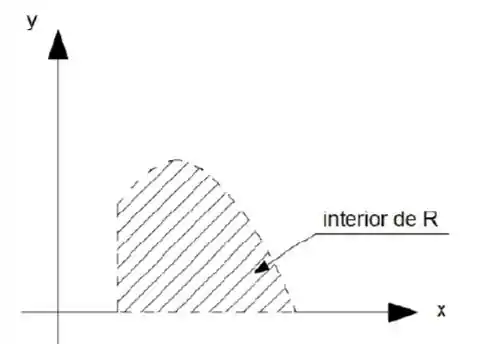
Considere a região do plano
- Desenhe (hachurando). Ao lado desenhe o interior de (pontilhando) e desenhe a fronteira de (tracejando). Determine a fronteira de , usando desigualdades e igualdades.
- Sabendo que a área de é dada por ; calcule a integral dupla abaixo:
- Seja a região do plano dada em . Calcule o volume da região definida por:
Passo 1
a) Vamos começar o nosso problema entendendo melhor as equações que a gente pode tirar das inequações que formam a região:
A gente sabe que representa uma reta paralela ao eixo e que passa justamente por (coincide com o nosso eixo ;).
De forma análoga, e são retas paralelas ao eixo e que passam justamente por esses valores de .
Mas calma! Quem é essa função seno mesmo?
Essa função é a função seno que a gente conhece, só que comprimida no eixo , se lembra dela? :)
Passo 2
Agora já podemos colocar tudo isso no plano cartesiano e representar o nosso R que está dentro dessas equações. Dessa forma:
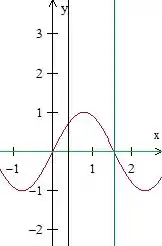
A gente pode representar a fronteira e o interior dessa forma:
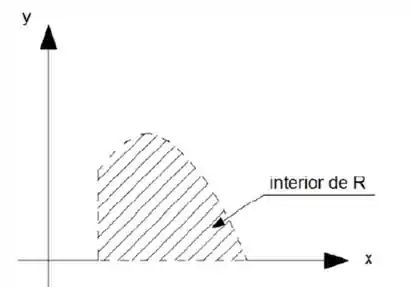
Passo 3
Por fim, e não morra de tédio, nossa fronteira é formada por nossas equações, basta delimitá-las:)
A nossa fronteira laranja está sob a curva do seno, porém, delimitada pelos e
Logo, estará bem representada por:
e são as fronteiras sob as retas e respectivamente.
A gente já sabe que a curva está limitada por e pela curva do seno. O nosso limite superior, será justamente a intercessão com essa curva
Assim, estará bem representada por
E de modo análogo, teremos para
Passo 4
b) muita calma nessa hora! Antes de começarmos a resolver a integral como um matemático louco, bora descrever essa região aí?
Podemos descrevê-la como uma região do Tipo 1, onde varia de até e varia de até a nossa função seno, ou seja:
Passo 5
Prontinho! :) Agora, vamos tentar deixar essa integral um pouco mais fácil separando em duas integrais pela propriedade da adição, dessa forma aqui
Começando pela integral , teremos
sabendo que representa a área da região, ganhamos
Passo 6
Para resolver a segunda integral, não tem por onde escapar: a gente tem que botar a mão na massa. Vem comigo montar a integral iterada:
Resolvendo primeiro a integral de dentro
Ganhamos essas duas integrais de fora, onde a primeira a gente obtém o resultado lembrando da nossa identidade trigonométrica
Dessa forma:
E resolvendo a segunda integral de fora por partes onde
Substituindo os limites de integração
Concluímos que
E juntando as duas integrais calculadas, encontramos a solução da integral pedida
Passo 7
c) Se a gente lembrar que volume sobre o gráfico de uma função até o plano é dado por , a gente terá que
A primeira integra a gente tem o resultado obtida no item anterior, basta somar com o dobro da área:)
Resposta