UFSCAR, Sem Campus, Cálculo 3, Listas de C3 - Profª Alessandra Verri - Lista 1, Questão 6b
Esboce o sólido cujo volume é dado pela integral
b)
Passo 1
Eaew, belezinha?
A questão nos pede para esboçar o sólido cujo volume é dado pela integral
. Primeiro, vamos analisar que superfície a função descreve: Se fizermos f(x,y) = z = k constante, temos que as curvas de nível obtidas com as interseções dos planos z = k são elipses com equações dadas por:
Onde o valor máximo assumido por k é igual à 9, visto que 3x²+2y² é sempre positivo ou nulo.
Se fizermos x = k, constante, temos que as curvas de interseção com a superfície são definidas pelas equações
Ou seja, no plano z-y, temos que as curvas de nível são parábolas com concavidade negativa. Temos algo semelhante para y = k constante, pois as curvas de interseção dos planos y = k com a superfície definida por f(x,y) são da forma:
Ou seja, temos novamente parábolas com concavidade negativa. Então, a superfície definida pela função f(x,y) é um parabolóide com concavidade negativa e seções transversais elípticas, como ilustra a figura abaixo:
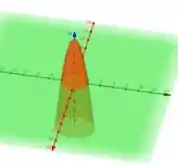
Agora, para esboçar o volume do sólido da integral, só precisamos desenhar os limites de integração do volume. Então bora lá!
Passo 2
Da integral vemos que os limites de integração para as duas variáveis x e y são 0 e 1. Então, o sólido cujo volume é dado pela integral nada mais é que o sólido contido entre os planos x = 0, x = 1 (em azul na figura a seguir), y = 0, y = 1 (em vermelho na figura abaixo) e a superfície descrita por f(x,y), em laranja na ilustração:
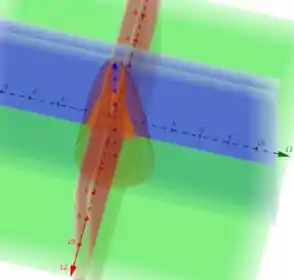
Resposta
Desenvolvida ao longo da questão.