Questão 2: Considere a região do espaço
c) Calcule o volume de .
Passo 1
ORA! Se quisermos o volume de um sólido, até o momento podemos calcular usando uma integral dupla!
Tudo que temos que fazer é encontrar quem são esses , e aí e montar a integral! Vamos nessa?
Passo 2
Acho interessante começarmos esse problema desenhando a região apenas para a gente ter uma noção geométrica do problema, vamos lá?
Poxa, esse aí é uma espécie de paraboloide, só que muito mais íngreme.
No entanto representa um cilindro de raio . O sinal de maior significa apenas que estamos pra fora dele.
A intersecção dos dois de até nos dá essa região aqui:
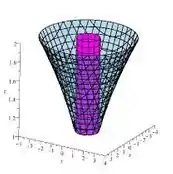
Perceba que quando , estamos na intersecção entre o cilindro e o “paraboloide íngreme”.
Passo 3
Ok, com isso a gente pode deve se recordar da Teoria e lembrar que as funções e representam as superfícies que estão por cima e a que está por baixo no sólido. No caso, observando novamente o nosso...
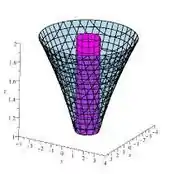
Dá pra perceber que por cima, o sólido está delimitado pelo plano, então...
E por baixo, temos uma delimitação pelo “paraboloide íngreme” de equação, logo a função ...
Falta só descobrir quem é a região neh? Vamos nessa?
Passo 4
Bem, a região de integração é a sombra (projeção) do sólido no plano :
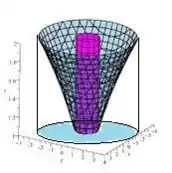
Essa sombra circular possui como bordas justamente as circunferências do limite inferior e superior do paraboloide...
Como o limite inferior é ...
E o superior... ...
Então estamos delimitados em um anel entre o raio e o raio :
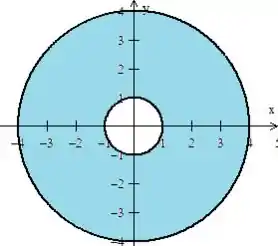
Passo 5
Ora, então se estamos trabalhando com uma região circular, nada mais justo que pensarmos nas coordenadas polares para facilitar a vida:
E a variação de e podem ser obtidos simplesmente observando a região de integração, onde a gente tira...
Passo 6
Então, de acordo com o passo estamos buscando essa integral aqui:
Substituindo as coordenadas polares não se esquecendo de multiplicar pelo jacobiano a função de integração...
Ok! Agora é só realmente calcularmos essa integral. Começando pela de dentro...