- Use uma integral dupla para calcular o volume do sólido limitado por:
Passo 1
Bem a primeira coisa que devemos fazer aqui é tentar entender um pouco mais sobre esse sólido . E não há nada melhor pra entendê-lo do que o desenhando no espaço. Bora?
Devemos começar desenhando cada uma dessas superfícies, vamos começar aqui essas duas mais fáceis. Veja!
- nos representa o próprio plano :
- Assim como a anterior, é o plano :
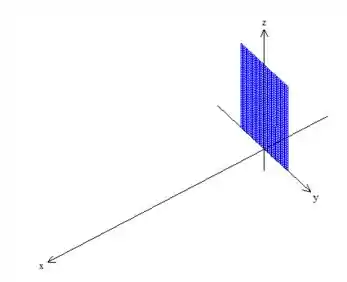
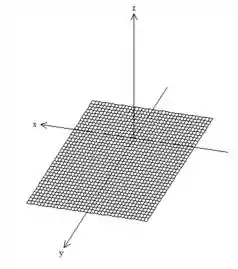
Agora, essa superfície , desenhamos um pouco diferente. Acompanha-me!
Passo 2
Para superfície que só dependem de duas incógnitas como , podemos sempre desenha-la no plano primeiro. No nosso caso, , note no plano nos representa uma reta e que vou desenha-la aqui pra você ohhh:
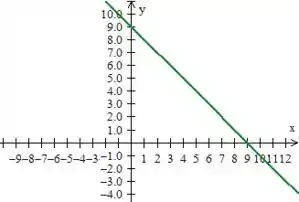
Colocando esse mesmo plano no espaço...
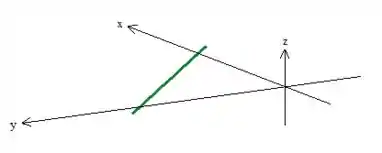
Pois bem! Agora como essa equação não depende de , o que deve ser feito é “puxar” essa reta aí em torno do eixo , saca? Então essa é a superfície:
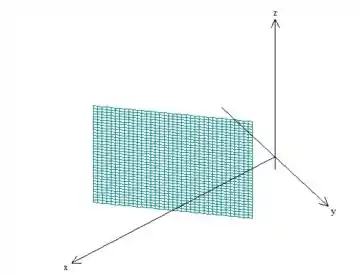
No caso... É um plano !
Passo 3
Agora façamos o mesmo com essa outra superfície, ! Vamos lá! Agora pra ver se você entendeu como desenhar esse tipo de superfície, heim!
Primeiro devemos...?
desenhar a equação no plano (no caso no plano ):
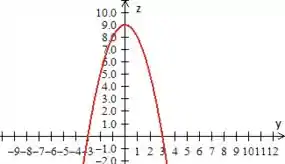
Depois devemos...?
“Puxar” essa reta em torno do outro eixo (no caso aqui é o ):
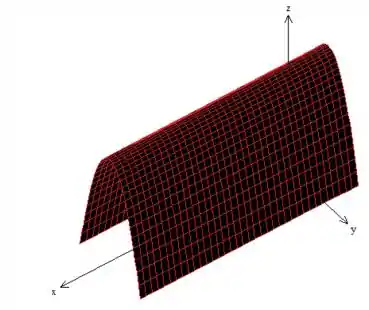
E prontinho! Esse é a superfície que carinhosamente chamamos de cilindro parabólico.
Passo 4
Wooooow! Cuidado, pois ainda não terminamos de ver o sólido! Temos que colocar essas coisas juntas. Assim, o nosso sólido é...
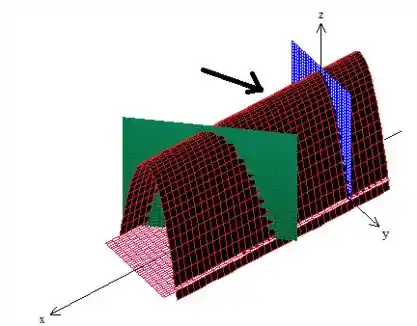
esse cara apontado por esta seta !
Passo 5
Para se calcular o volume desse pedacinho , como você já sabe, devemos aplicar a fórmula do volume:
Onde se percebe que precisamos obter algumas informações cruciais para matar a questão:
- Precisamos saber quem é essa função a ser integrada.
- Além disso, precisamos saber quem é a região de integração.
Para ambas as questões, basta que olhemos para o sólido novamente e com mais cautela:
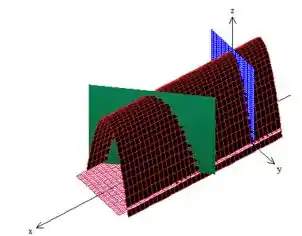
Repare que a função que devemos integrar, , é exatamente esse cilindro parabólico que é o teto do sólido, , percebeu?
Enquanto que a região de integração nada mais é do que a sombra desse “teto” no plano , o que formalmente chamamos de projeção no plano! Veja ;0
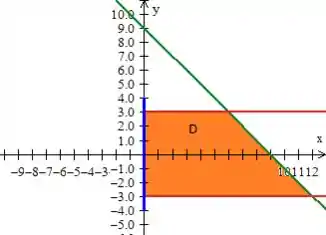
Ou melhor...
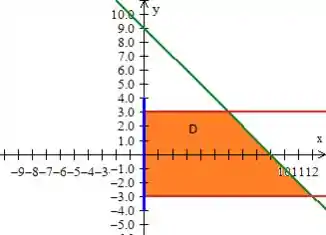
Essas retas vermelhas são facilmente obtidas fazendo a intercessão do cilindro vermelho,, com o plano :
Descrevendo então essa região aí... (nesse caso pode ser como do tipo ):
enquanto isso...
Substituindo esses dados na integral dupla, ganhamos...
Passo 6
Para resolver essa integral, calculemos primeiro a integral de dentro...
como é uma função que só depende de, ela pode cair fora da integral de dentro...
substituindo os limites em ...
Integrando...
substituindo...
simplificando tudo...