Determinar o volume do sólido limitado pelo cilindro e pelos planos e .
Passo 1
Beleza, vamos começar tentando fazer um esboço da região.
A primeira equação é a mais simples, ela descreve um cilindro de raio em torno do eixo :
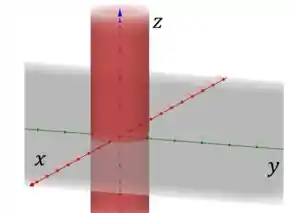
A equação é esse plano cinzento que já está aí no desenho. A gente só está interessado na região que está acima dele.
Mas e essa equação aqui?
Bom, quando estamos no espaço ela é um plano, mas a equação parece a dessa reta aqui:
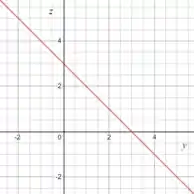
Para desenhar isso no espaço, é só prolongar essa reta ao longo do eixo , então:
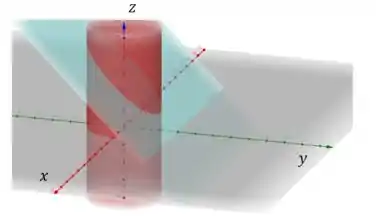
Beleza, já temos a região desenhada, agora vamos tentar escrever isso matematicamente.
Passo 2
A nossa estratégia vai ser a seguinte: a gente vai usar a integral dupla pra percorrer aquele círculo de raio que está no plano .
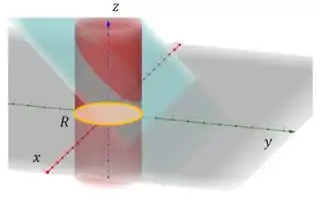
E pra cada ponto nesse círculo , nós vamos calcular a altura até aquele plano azul. Quando a gente somar essa altura sobre cada ponto no círculo , vamos ter o volume da região!
Como a gente pode expressar aquela altura? Bom, nesse caso, “altura” é simplesmente a coordenada , então vamos usar a própria equação do plano:
Então:
Ok, agora é só integrar essa função sobre o círculo .
Passo 3
Pra fazer isso, vamos usar coordenadas polares. Temos que usar essa transformação aqui:
E usar o Jacobiano para trocar :
Então:
E agora, como escrever os limites de integração? Bom, pra percorrer um círculo de raio , temos que usar esses limites aqui:
Então:
Agora vamos resolver!
Passo 4
Primeiro vamos integrar em relação a :
Aqui só temos a integral de um polinômio, então:
Substituindo isso na integral:
Agora vamos integrar em relação a :
A primeira integral dá:
E a segunda integral:
Então:
Resposta
O volume do sólido é .