UFU, Sem Campus, Cálculo 2, Listas de C2 - Profª Ana Paula - Lista 7 - Integrais Duplas, Questão 9a
Determine o volume do sólido dado
- Abaixo do plano e acima da região limitada por e .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcular o volume do sólido abaixo do plano e acima da região limitada por e .
Lembrando que o volume do sólido limitado por uma superfície e abaixo pelo plano é expressa através da seguinte integral dupla:
Em que é a região limitada no plano em que devemos integrar a função.
Eaí? Bora lá?
😉
Passo 2
Assim, esboçando a região, temos:
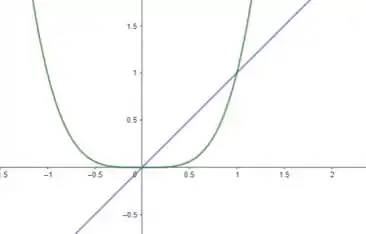
Calculando a intersecção das curvas:
e
Assim, analisando o gráfico e os ponto de intersecção, obtemos nossa integral dupla:
Integrando com relação a :
Agora, integrando com relação a :
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Encontre a área da superfície com precisão de quatro casas decimais expressando a área em termos de uma integral simples e usando uma calculadora para estimar a integral.A parte da superfície z = 1 /
Use um sistema de computação algébrico para determinar o volume exato do sólido.Delimitado por z = x 2 + y 2 e z = 2 y .
Utilize coordenadas polares para determinar o volume do sólido dado.Limitado pelo paraboloide z = 1 + 2 x 2 + 2 y 2 e pelo plano z = 7 no primeiro octante
Desenhe o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 4 - x - 2 y d x d y
Nos Exercícios 67 e 68, esboce a região de integração e o sólido cujo volume seja dado pela integral dupla.