Calcule o volume do sólido definido por , onde
Passo 1
Faala, pessoal! Vamos compreender melhor a figura que define o limite do volume. A cada altura , temos um raio máximo ao qual podemos obter.
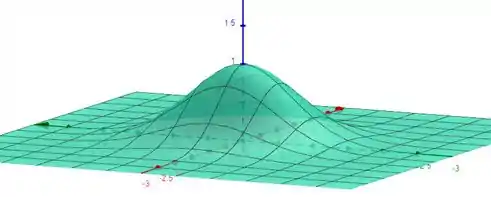
Assim, se integrarmos discos paralelos ao plano de raio e espessura , teremos:
Aplicando o método da integração por partes, temos:
Logo,
Substituindo , temos:
Onde o limite evidenciado vale , devido ao fato de funções polinomiais crescerem mais rápido que logarítmicas.