Questão 2: Determine o volume do sólido abaixo da superfície e acima do triângulo com vértices , , .
Passo 1
Bem, se queremos calcular volume, então o que o problema quer que a gente calcule aqui na verdade é uma integral dupla dessa forma aqui:
O que nos falta saber é quem essa e saber também quem é essa região . Vamos nessa?
Passo 2
Primeiro vamos definir aqui quem é a função de integração.
Mas relaxa! Não é um monstro de cabeças sabe por quê? Por que a função de integração é a função que a gente quer calcular o volume entre ela e o plano onde está a região de integração . Como o nosso problema já nos disse, queremos o volume abaixo de
Então essa superfície será a , saca?
Passo 3
SIM! Agora vamos falar um pouquinho da nossa região de integração: o problema já nos informou quem é ela:
“... acima do triângulo com vértices , , .”
Então vamos desenha-lo!
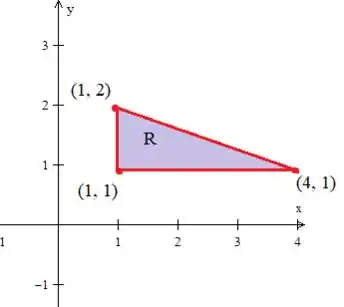
Veja que o nosso problema não é nem desenha-la, mas será em descrevê-la. Porém, não se preocupe, vou te ajudar a conseguir acabar com questões desse tipo na sua prova. Vem comigo!
Passo 4
Podemos descrever essa região como sendo do TIPO 1, afinal podemos colocar o nosso varia em um intervalo numérico do ponto onde começa até o último da nossa região...
Agora o , eu quero que você veja que ele está variando de uma base a um teto. A base, basicamente é o lado do triângulo paralelo ao eixo com . Já o Teto, é a hipotenusa do triângulo, nesse caso:
A grande pergunta é: como encontramos a equação dessa hipotenusa?
Passo 5
Tem um jeito que é o seguinte: sabemos que a hipotenusa é uma reta e, portanto, ela deve ter uma cara assim:
Onde e são constantes que temos que encontrar. Temos dois pontos que pertencem a essa reta () e como toda reta depende de dois pontos para ser determinada, vamos substitui-los nessa equação:
Isolando em cima e trocando em baixo...
E
Logo, a reta que vamos ter é...
Então podemos falar sem medo que essa é a equação do teto...
Passo 6
Com isso tudo definido:
e
Podemos jogar na integral dupla...
Integrando a de dentro considerando constante...
Substituindo...
Simplificando um pouco...