UFSCAR. Cálculo 3. Lista de Estudos – Integrais Duplas. Questão 8.
8 – Calcule o volume do sólido delimitado pelas superfícies dadas por , e .
Passo 1
Fala aí! Tudo belezinha por aí? Vamos resolver mais essa questão juntos? Vem comigo!
Bem, o problema pediu pra gente calcular volume do sólido delimitado pelas superfícies dadas por , e .
Bom, o primeiro passo será entender que região é essa, e para isso nós teremos que desenhá-la. Então bora fazer isso.
Passo 2
Vamos começar desenhando
Perceba que essa é a equação de um cilindro e seu gráfico é o seguinte:
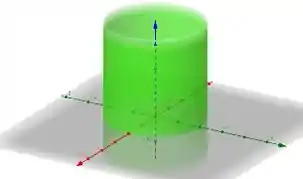
Agora vamos desenhar a curva , que é o próprio plano .
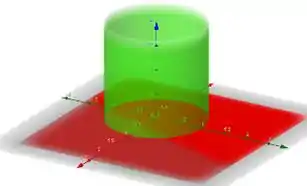
E, por fim, vamos colocar a curva que é o paraboloide.
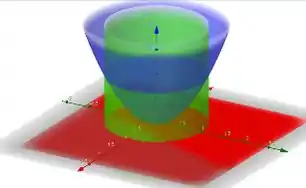
Repara que ao fazermos o desenho das curvas, conseguimos perceber melhor o sólido que se forma com a limitação da região.
Então, analisando que a curva que limita o sólido superiormente é o paraboloide, lateralmente é o cilindro e inferiormente o plano . Assim, para calcular o volume desse sólido, basta resolver a integral dupla do paraboloide na região limitada dela intersecção entre o cilindro e a plano .
Passo 3
A integral se torna:
Em que é a intersecção entre o cilindro e o plano , ou seja:
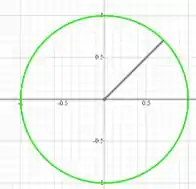
Passo 4
Usando coordenada polares, teremos:
E os limites de integração serão:
E para
E nossa integral será:
Resolvendo, teremos
E finalmente, integral resolvida.
Depois dessa, toma uma aguinha e volta pra gente continuar. Ok?!